Cho hàm số y = 1 x . Khi đó y n bằng (đạo hàm cấp n của hàm số)
![]()
![]()
![]()
![]()
Cho hàm số y = 1 x . Khi đó y n x bằng (đạo hàm cấp n của hàm số)
A. y n x = − 1 n n ! x n + 1
B. y n x = n ! x n + 1
C. y n x = − 1 n n ! x n
D. y n x = n ! x n
Cho hàm số y = 1 x . Khi đó y n x bằng (đạo hàm cấp n của hàm số)
A. y n x = − 1 n n ! x n + 1
B. y n x = n ! x n + 1
C. y n x = − 1 n n ! x n
D. y n x = n ! x n
Đáp án A
Ta có y ' = − 1 x 2 = − 1 1 . 1 ! x 2 ; y ' ' = − 2 x 3 = − 1 2 . 2 ! x 3 ; y ' ' ' = − 6 x 4 = − 1 3 . 3 ! x 4 .
Dự đoán y n = − 1 n . n ! x n + 1 * . Chứng minh mệnh đề (*):
* Với n=1 thì * ⇔ y ' = − 1 x 2 . Khi đó (*) đúng.
* Giả sử (*) đúng với n = k , k ≥ 1 , tức là y k = − 1 k . k ! x k + 1 .
Khi đó y k + 1 = y k ' = − 1 k . k ! x k + 1 = − 1 k . − k + 1 . k ! . x k x k + 1 2 = − 1 k + 1 . k + 1 ! x k + 2 . Vậy mệnh đề (*) cũng đúng với n=k+1 nên nó đúng với mọi n.
a) Dùng định nghĩa tỉnh đạo hàm của hàm số \(y = x\) tại điểm \(x = {x_0}\).
b) Nhắc lại đạo hàm của các hàm số \(y = {x^2},y = {x^3}\) đã tìm được ở bài học trước. Từ đó, dự đoán đạo hàm của hàm số \(y = {x^n}\) với \(n \in {\mathbb{N}^*}\).
a) Với bất kì \({x_0} \in \mathbb{R}\), ta có:
\(f'\left( {{x_0}} \right) = \mathop {\lim }\limits_{x \to {x_0}} \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} \frac{{x - {x_0}}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} 1 = 1\)
Vậy \(f'\left( x \right) = {\left( x \right)^\prime } = 1\) trên \(\mathbb{R}\).
b) Ta có:
\(\begin{array}{l}{\left( {{x^2}} \right)^\prime } = 2{\rm{x}}\\{\left( {{x^3}} \right)^\prime } = 3{{\rm{x}}^2}\\...\\{\left( {{x^n}} \right)^\prime } = n{{\rm{x}}^{n - 1}}\end{array}\)
Tính đạo hàm cấp n của hàm số y = 2 x + 1
A. 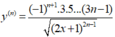
B. 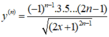
C. 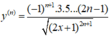
D. 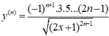
Cho hàm số liên tục trên khoảng (a;b) và x 0 ∈ ( a ; b ) . Có bao nhiêu mệnh đề đúng trong các mệnh đề sau?
(1) Hàm số đạt cực trị tại điểm x 0 khi và chỉ khi f ' ( x 0 ) = 0 .
(2) Nếu hàm số y = f ( x ) có đạo hàm và có đạo hàm cấp hai tại điểm x 0 thỏa mãn điều kiện f ' ( x 0 ) = f ' ' ( x 0 ) = 0 thì điểm x 0 không phải là điểm cực trị của hàm số y = f ( x ) .
(3) Nếu f'(x) đổi dấu khi x qua điểm x 0 thì điểm x 0 là điểm cực tiểu của hàm số y = f ( x ) .
(4) Nếu hàm số y = f ( x ) có đạo hàm và có đạo hàm cấp hai tại điểm x 0 thỏa mãn điều kiện f ' ( x 0 ) = 0 , f ' ' ( x 0 ) > 0 thì điểm x 0 là điểm cực tiểu của hàm số y = f ( x ) .
A. 1
B. 2
C. 0
D. 3
Đáp án A
Phương pháp:
Dựa vào khái niệm cực trị và các kiến thức liên quan.
Cách giải:
(1) chỉ là điều kiện cần mà không là điều kiện đủ.
VD hàm số y = x3 có y' = 3x2 = 0 ⇔ x = 0. Tuy nhiên x = 0 không là điểm cực trị của hàm số.
(2) sai, khi f''(x0) = 0, ta không có kết luận về điểm x0 có là cực trị của hàm số hay không.
(3) hiển nhiên sai.
Vậy (1), (2), (3): sai; (4): đúng
Cho hàm số liên tục trên khoảng (a;b) và x 0 ∈ a ; b . Có bao nhiêu mệnh đề đúng trong các mệnh đề sau ?
(1) Hàm số đạt cực trị tại điểm x 0 khi và chỉ khi f ' x 0 = 0
(2) Nếu hàm số y = f(x) có đạo hàm và có đạo hàm cấp hai tại điểm x 0 thỏa mãn điều kiện f ' x 0 = f " x 0 = 0 thì điểm x 0 không là điểm cực trị của hàm số y = f x
(3) Nếu f'(x) đổi dấu khi x qua điểm x 0 thì điểm x 0 là điểm cực tiểu của hàm số y = f(x)
(4) Nếu hàm số y = f(x) có đạo hàm và có đạo hàm cấp hai tại điểm x 0 thỏa mãn điều kiện f ' x 0 = 0 , f " x 0 > 0 thì điểm x 0 là điểm cực đại của hàm số y = f(x)
A. 1
B. 2
C. 0
D. 3
Cho hàm số y = f x liên tục trên khoảng a ; b và x 0 ∈ a ; b . Có bao nhiêu mệnh đề đúng trong các mệnh đề sau
(1). Hàm số đạt cực trị tại điểm x 0 khi và chỉ khi f ' x 0 = 0
(2). Nếu hàm số y = f x có đạo hàm và có đạo hàm cấp hai tại điểm x 0 thoả mãn điều kiện f ' x 0 = f ' ' x 0 = 0 thì điểm x 0 không phải là điểm cực trị của hàm số y = f x
(3). Nếu f ' x đổi dấu khi x qua x 0 thì điểm x 0 là điểm cực tiểu của hàm số y = f x
(4). Nếu hàm số y = f x có đạo hàm và có đạo hàm cấp hai tại điểm x 0 thoả mãn điều kiện f ' x 0 = 0 ; f ' ' x 0 > 0 thì điểm x 0 là điểm cực đại của hàm số y = f x
A. 0
B. 1
C. 2
D. 3
Đáp án A
A sai vì hàm số y = x 3 có y ' 0 = 0 nhưng không đạt cực trị tại x = 0
B sai vì hàm số y = x 4 có y ' 0 = 0 , y ' ' 0 = 0 đạo hàm và có đạo hàm cấp hai tại điểm x 0 thoả mãn điều kiện f ' x 0 = f ' ' x 0 = 0 thì điểm x 0 nhưng không đạt cực trị tại x = 0
C sai vì “Nếu f ' x đổi dấu khi x qua x 0 thì điểm x 0 là điểm trị (cực đại và cực tiểu) của hàm số y = f ' ' x
D sai vì “Nếu hàm số y = f x có đạo hàm và có đạo hàm cấp hai tại điểm x 0 thoả mãn điều kiện f ' x 0 = 0 ; f ' ' x 0 > 0 thì điểm x 0 là điểm cực đại của hàm số y = f ' ' x
Cho hàm số y = f x liên tục trên khoảng a ; b và x 0 ∈ a ; b . Có bao nhiêu mệnh đề đúng trong các mệnh đề sau
1) Hàm số đạt cực trị tại điểm x 0 khi và chỉ khi f ' x 0 = 0 .
2) Nếu hàm số y = f x có đạo hàm và có đạo hàm cấp hai tại điểm x 0 thoả mãn điều kiện f ' x 0 = f ' ' x 0 = 0 thì điểm x 0 không phải là điểm cực trị của hàm số y = f x .
3) Nếu f ' x đổi dấu khi x qua điểm x 0 thì điểm x 0 là điểm cực tiểu của hàm số y = f x .
4) Nếu hàm số y = f x có đạo hàm và có đạo hàm cấp hai tại điểm x 0 thoả mãn điều kiện f ' x 0 = 0 , f ' ' x 0 > 0 thì điểm x 0 là điểm cực đại của hàm số y = f x .
A. 0.
B. 1.
C. 2.
D. 3.
Đáp án A
Mệnh đề 1) sai vì f ' x 0 = 0 chỉ là điều kiện cần chưa là điều kiện đủ để hàm số đạt cực trị tại x 0
Mệnh đề 2) Sai vì khi f ' x 0 = f ' ' x 0 = 0 có thể hàm số có thể đạt cực trị hoặc không đạt cực trị tại x 0 .
Mệnh đề 3) sai vì f ' x đổi dấu qua điểm x 0 thì điểm x 0 có thể là điểm cực đại hoặc điểm cực tiểu của hàm số.
Mệnh đề 4) Sai vì trong trường hợp này x 0 là điểm cực tiểu của đồ thị hàm số.
Cho em hỏi câu này với ạ!
Tính đạo hàm cấp n của hàm số: y=(4x+1)^n
e cảm ơn!!!.
\(\sqrt[n]{y}=4x+1\)
\(y^{\dfrac{1}{n}}=4x+1\)
đạo cấp 1
\(\dfrac{1}{n}y^{\left(\dfrac{1}{n}-1\right)}=\dfrac{1}{n}\sqrt[n]{y^{\left(1-n\right)}}=4\)
thay y=(4x+1)^n vào
\(\dfrac{1}{n}\sqrt[n]{\left(4x+1\right)^{n\left(1-n\right)}}=\dfrac{1}{n}\left(4x+1\right)^{\left(1-n\right)}\)
từ đó: \(y'=\dfrac{4}{\dfrac{1}{n}\left(4x+1\right)^{\left(1-n\right)}}=4.n\left(4x+1\right)^{n-1}\)
Có đúng không: cấp n có thể phải làm lấy vài cái--> quy luật nào đó