Tập giá trị của hàm số y = x - 3 + 7 - x là
A. [3;7]
B. [3; 2 2 ]
C. (3,7)
D. [2; 2 2 ]
PB
Những câu hỏi liên quan
Tập giá trị của hàm số
y
x
−
3
+
7
−
x
là: A.
2
;
2
2
B. [3;7] C.
0
;
2
2
D. (3;7)
Đọc tiếp
Tập giá trị của hàm số y = x − 3 + 7 − x là:
A. 2 ; 2 2
B. [3;7]
C. 0 ; 2 2
D. (3;7)
Phương pháp:
Tìm TXĐ của hàm số sau đó xét sự biến thiên, lập BBT và tìm tập giá trị của hàm số.
Cách giải:
Đúng 0
Bình luận (0)
Cho bài toán: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số
y
2
x
4
−
4
x
2
+
3
. Dưới đây là lời giải của học sinh:* Bước 1: Tập xác định
D
ℝ
. Đạo hàm
y
8
x
3
−
8
x
.* Bước 2: Cho
y...
Đọc tiếp
Cho bài toán: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = 2 x 4 − 4 x 2 + 3 . Dưới đây là lời giải của học sinh:
* Bước 1: Tập xác định D = ℝ . Đạo hàm y ' = 8 x 3 − 8 x .
* Bước 2: Cho y ' = 0 tìm x = 0 ; x = − 1 ; x = 1 .
* Bước 3: Tính y 0 = 3 ; y − 1 = y 1 = 1 . Vậy giá trị lớn nhất của hàm số là 3, và giá trị nhỏ nhất là 1.
Lời giải trên đúng hay sai? Nếu sai thì giải sai từ bước mấy?
A. Bước 2
B. Lời giải đúng
C. Bước 3
D. Bước 1
Đáp án C
Lời giải trên là sai. Cách làm lời giải này chỉ đúng đối với bài toán tìm giá trị lớn nhất – giá trị nhỏ nhất của hàm số trên một đoạn .
Để giải bài toán này, ta lập bảng biến thiên của hàm số y = 2 x 4 − 4 x 2 + 3 trên R
* Bước 1: Tập xác định D = ℝ . Đạo hàm y ' = 8 x 3 − 8 x .
* Bước 2: Cho y ' = 0 tìm x = 0 ; x = − 1 ; x = 1 .
* Bước 3: Ta có bảng biến thiên sau:
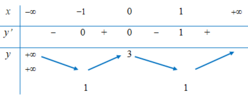
Quan sát bảng biến thiên, ta thấy giá trị nhỏ nhất của hàm số là 1 và hàm số không có giá trị lớn nhất. Vậy lời giải trên sai từ bước 3.
Đúng 0
Bình luận (0)
Cho hàm số f(x)3sinx +3. Gọi S là tập hợp các giá trị nguyên của tham số m để hàm số
y
f
3
(
x
)
-
3
m
f
2
(
x
)
+
3
(
m
2
-
4
)
f
(
x
)
-
m
nghịch biến trên khoảng
(
0
;...
Đọc tiếp
Cho hàm số f(x)=3sinx +3. Gọi S là tập hợp các giá trị nguyên của tham số m để hàm số y = f 3 ( x ) - 3 m f 2 ( x ) + 3 ( m 2 - 4 ) f ( x ) - m nghịch biến trên khoảng ( 0 ; π 2 ) . Số tập con của S bằng
Bài 1: Cho hàm số : y x −3 có đồ thị là đường thẳng (d) 1
a/ Tính giá trị hàm số khi x0; x−3x 1/3
b/ Tìm giá trị của biến số x khi y0;y-7^3
c/ Xác định hệ số góc của đường thẳng d . Góc tạo bởi d và trục Ox là góc nhọn hay tù?
d/. Cho biết tọa độ các giao điểm A,B của đồ thị với trục tung và trục hoành .
e/ Vẽ đồ thị hàm số g/ Tính OA;OB và AB.
Đọc tiếp
Bài 1: Cho hàm số : y = x −3 có đồ thị là đường thẳng (d) 1
a/ Tính giá trị hàm số khi x=0; x=−3x= 1/3
b/ Tìm giá trị của biến số x khi y=0;y=-7^3
c/ Xác định hệ số góc của đường thẳng d . Góc tạo bởi d và trục Ox là góc nhọn hay tù?
d/. Cho biết tọa độ các giao điểm A,B của đồ thị với trục tung và trục hoành .
e/ Vẽ đồ thị hàm số g/ Tính OA;OB và AB.
Cho hàm số y=(5-3\(\sqrt{ }\)2)x+\(\sqrt{ }\)2 -1
a) Hàm số đã cho đồng biến hay nghịch biến trên tập?vì sao
b) Tính giá trị của y khi x=5+3\(\sqrt{ }\)2
c) Tìm các giá trị của x khi y=0
a, Vì \(5-3\sqrt{2}>0\) nên hs đồng biến trên R
b, \(x=5+3\sqrt{2}\Leftrightarrow y=25-18+\sqrt{2}-1=6+\sqrt{2}\)
c, \(y=0\Leftrightarrow\left(5-3\sqrt{2}\right)x+\sqrt{2}-1=0\Leftrightarrow x=\dfrac{1-\sqrt{2}}{5-3\sqrt{2}}\)
\(\Leftrightarrow x=\dfrac{\left(1-\sqrt{2}\right)\left(5+3\sqrt{2}\right)}{7}=\dfrac{-2\sqrt{2}-1}{7}\)
Đúng 0
Bình luận (0)
Cho hàm số f(x)3 sinx+2. Gọi S là tập hợp các giá trị nguyên của tham số m để hàm số
y
f
3
(
x
)
-
3
mf
2
(
x
)
+
3
(
m...
Đọc tiếp
Cho hàm số f(x)=3 sinx+2. Gọi S là tập hợp các giá trị nguyên của tham số m để hàm số y = f 3 ( x ) - 3 mf 2 ( x ) + 3 ( m 2 - 4 ) f ( x ) - m nghịch biến trên khoảng (0;π/2). Số tập con của S bằng
A. 1
B. 2.
C. 4.
D. 16.
Cho hàm số y = x 3 - 3 ( m + 1 ) x 2 + 3 ( 7 m - 3 ) x . Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để hàm số không có cực trị. Số phần tử của S là
A. 2
B. 4
C. 0
D. Vô số
cho hàm số bậc nhất y=( căn 3-2)x +5
a) hàm số trên là đồng biến hay nghịch biến trên R? Vì sao?
b) tính giá trị của x khi y=căn 3-7
a)
Ta thấy \(\sqrt{3}-2< 0\) nên hàm số trên nghịch biến trên R
b)
\(\sqrt{3}-7=\left(\sqrt{3}-2\right)x+5\)
\(\Leftrightarrow\sqrt{3}-12=\left(\sqrt{3}-2\right)x\)
\(\Leftrightarrow x=\dfrac{\sqrt{3}-12}{\sqrt{3}-2}\)
Đúng 1
Bình luận (0)
Gọi A là tập hợp các giá trị nguyên của tham số m để hàm số
y
x
+
1
2
x
+
m
đồng biến trên khoảng . Số tập hợp con của tập hợp A gồm 3 phần tử bằng A. 816. B. 364. B. 286. C. 455.
Đọc tiếp
Gọi A là tập hợp các giá trị nguyên của tham số m để hàm số y = x + 1 2 x + m đồng biến trên khoảng . Số tập hợp con của tập hợp A gồm 3 phần tử bằng
A. 816.
B. 364.
B. 286.
C. 455.
Chọn đáp án B.
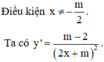
Hàm số đã cho đồng biến trên khoảng - ∞ ; - 8
Do đó, số tập con gồm 3 phần tử của tập hợp A là C 14 3 = 364
Đúng 0
Bình luận (0)