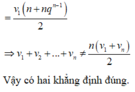Cho cấp số cộng (un) có u 1 = - 2 và công sai d = 5. Số 198 là số hạng thứ bao nhiêu của cấp số cộng?
A. Thứ 25.
B. Thứ 39.
C. Thứ 40.
D. Thứ 41.
Theo đề, ta có: \(S_n=3003\)
=>\(n\cdot\dfrac{\left[2u1+\left(n-1\right)\cdot d\right]}{2}=3003\)
=>\(\dfrac{n\left[2+\left(n-1\right)\right]}{2}=3003\)
=>n(n+1)=6006
=>n^2+n-6006=0
=>(n-77)(n+78)=0
=>n=77(nhận) hoặc n=-78(loại)
Vậy: n=77
Cho cấp số cộng ( u n ) có số hạng tổng quát là u n = 3 n - 2 . Tìm công sai d của cấp số cộng
A. d = 3
B. d = 2
C. d = - 2
D. d = - 3
Chọn đáp án A.
Ta có u n + 1 - u n = 3 ( n + 1 ) - 2 - 3 n + 2 = 3
Suy ra d = 3 là công sai của cấp số cộng
Cho cấp số cộng u n có số hạng tổng quát là u n = 3 n - 2 . Tìm công sai d của cấp số cộng.
A. d = 3
B. d = 2
C. d = - 2
D. d = - 3
Cho các dãy số (un) sau :
1. u n = 3 n + 1
2. u n = 4 − 5 n
3. u n = 2 n + 3 5
4. u n = n + 1 n
Hỏi có bao nhiêu dãy số là cấp số cộng ?
A. 1
B. 2
C.3
D.4
Chọn C
1. u n = 3 n + 1 2. u n = 4 − 5 n
3. u n = 2 n + 3 5 4. u n = n + 1 n
* Xét dãy số: u n = 3 n + 1
Ta có:
u n + 1 − u n = 3 ( n + 1 ) + 1 − 3 n − 1 = 3
Dãy số này là cấp số cộng có công sai d= 3.
* Xét dãy số u n = 4 − 5 n .
Ta có:
u n + 1 − u n = 4 − 5 ( n + 1 ) − ( 4 − 5 n ) = − 5
Dãy số này là cấp số cộng có công sai d = -5
* Xét dãy số u n = 2 n + 3 5
Ta có:
u n + 1 − u n = 2 ( n + 1 ) + 3 5 − 2 n + 3 5 = 2 5 .
Dãy (un) là cấp số cộng có công sai d = 2 5
* Xét dãy số u n = n + 1 n
Ta có:
u n + 1 − u n = n + 1 + 1 n + 1 − n + 1 n = ( n + 2 ) . n − ( n + 1 ) 2 n . ( n + 1 ) = − 1 n ( n + 1 ) ⇒ ( u n )
không là cấp số cộng
Cho cấp số cộng u n có u 1 = - 1 công sai d=2. Gọi S n là tổng n số hạng đầu tiên của cấp số cộng. Tỷ số S 2018 S 2019 bằng
A. 2018 2 - 1 2019 2 - 1
B. 2016 2 - 1 2017 2 - 1
C. 2017 2 - 1 2018 2 - 1
D. 2019 2 - 1 2010 2 - 1
Hmm, cái công thức Sn mỗi lần viết dài kinh :(
\(u_5=u_1+4d=15;u_9=u_1+8d=-1\) \(\Rightarrow\left\{{}\begin{matrix}d=...\\u_1=...\end{matrix}\right.\)
\(\Rightarrow u_{100}=u_1+99d=...\)
\(u_1=u_1\)
\(u_2=u_1+d\)
\(u_3=u_1+2d\)
.....
\(u_n=u_1+\left(n-1\right)d\)
\(\Rightarrow S_n=u_1+u_2+...+u_n=u_1+u_1+d+...+u_1.\left(n-1\right)d=n.u_1+d+2d+...+\left(n-1\right)d\)
\(=n.u_1+\left(1+2+...+\left(n-1\right)\right)d=n.u_1+\dfrac{d\left(n-1\right).n}{2}=\dfrac{n\left[2u_1+\left(n-1\right)d\right]}{2}\)
Thay số vô và ... bấm máy, chắc zậy :))
Cho cấp số cộng ( u n ) có u 3 = 15 và d= -2. Tìm u n ?
A. u n = − 2 n + 21.
B. u n = − 3 2 n + 12.
C. u n = − 3 n − 17.
D. u n = 3 2 n 2 − 4.
Ta có 15 = u 3 = u 1 + 2 d d = − 2 ⇔ u 1 = 19 d = − 2
⇒ u n = u 1 + n − 1 d = 19 + ( n − 1 ) . ( − 2 ) = − 2 n + 21.
Chọn đáp án A
Cho cấp số cộng (un) có d = -2 và S8 = 72. Số hạng đầu tiên của cấp số cộng bằng
A. - 1 16
B. 1 16
C. 16
D. -16.
Cho cấp số cộng (un) có d = -2 và S8 = 72. Số hạng đầu tiên của cấp số cộng bằng
A. - 1 16
B. 1 16
C. 16
D. -16
Chọn đáp án C.
Có S 8 = 8 2 ( 2 u 1 + ( 8 - 1 ) d )
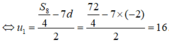
Cho u n là cấp số cộng có công sai là d, v n là cấp số nhân có công bội là q và các khẳng định
I ) u n = d + u n − 1 ∀ n ≥ 2, n ∈ N
I I ) v n = q n v 1 ∀ n ≥ 2, n ∈ N
I I I ) u n = u n − 1 + u n + 1 2 ∀ n ≥ 2, n ∈ N
I V ) v n − 1 v n = v n − 1 2 ∀ ≥ 2, n ∈ N
Có bao nhiêu khẳng định đúng trong các khẳng định trên?
A. 4
B. 2
C. 3
D. 5
Đáp án B
Phương pháp: Dựa vào định nghĩa và các tính chất của các số cộng và cấp số nhân.