Cho số phức z thỏa mãn 2 + 4 i z + 2 = 4 + 3 i z + i Modun của số phức z là
A . z = 5 2
B . z = 2
C . z = 1
D . z = 3 2
Câu 1 : Cho số phức \(z\) thỏa mãn \(z\) + ( 2 - i )\(\overline{z}\) = 3 - 5i. Môđun của số phức w = \(z \) - i bằng bao nhiêu ?
Câu 2 : Cho số phức \(z\) = a + bi, (a,b ∈ R ) thỏa mãn ( 3 + 2i )\(z\) + ( 2 - i )2 = 4 + i. Tính P = a - b
Cho số phức z thỏa mãn điều kiện ( 3 + 2 i ) z + ( 2 - i ) 2 = 4 + i . Tìm phần ảo của số phức w = ( 1 + + z ) z ¯ .
A. -2
B. 0.
C. -1
D. 1
Cho số phức z thỏa mãn điều kiện ( 3 + 2 i ) z + ( 2 - i ) 2 = 4 + i . Tìm phần ảo của số phức w = ( 1 + z ) z ¯ .
![]()
![]()
![]()
![]()
Cho số phức z thỏa mãn ( 1+ i) z + 2z = 2. Tính mô-đun của số phức w = z + 2/5 - 4/5i.
A. 1.
B. 2.
C. 2
D. 3
Chọn C.
Đặt z = a+ bi.
Theo đề ra ta có: ( 3 + i) z = 2
Hay ( 3 + i)( a + bi) = 2
Suy ra: 3a - b + ( 3b + a) i = 2
![]()
nên z = 3/5 - 1/5i.
Khi đó w = 3/5 - 1/5i + 2/5 - 4/5 i = 1 - i.
Vậy ![]()
Cho số phức z thỏa mãn |z - 2 + 3i| + |z - 2 + i| = 4 5 . Tính GTLN của P = |z - 4 + 4i|
A. maxP = 4 5
B. maxP = 7 5
C. maxP = 5 5
D. maxP = 6 5
Đáp án A
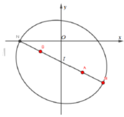
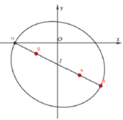
Cho số phức z = x + yi (x,y ∈ R) , S(x,y) là điểm biểu diễn của z trên hệ trục tọa độ Oxy
![]()
![]()
Lấy các điểm A(2; - 3), B( - 2; - 1)
Phương trình
![]()
=> Tập hợp các điểm S là đường elip (E) có tiêu điểm A(2;
-
3), B(
-
2;
-
1) và có độ dài trục lớn là ![]()
Lấy M(4;
-
4). Dễ dàng kiểm tra được 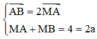
Suy ra, M là một đỉnh và nằm trên trục lớn của elip (E).
Gọi I là trung điểm AB => I(0;
-
2), N là điểm đối xứng của M qua I. Khi đó, với mọi điểm ![]()
![]() khi và chỉ khi S trùng N
khi và chỉ khi S trùng N ![]() khi và chỉ khi
khi và chỉ khi ![]()
Cho số phức z thỏa mãn z - 2 + 3 i + z - 2 + i = 4 5 Tính GTLN của P = z - 4 + 4 i
![]()
![]()
![]()
![]()
Cho số phức z thỏa mãn z - 2 + 3 i + z - 2 + i = 4 5 .
Tính GTLN của P = z - 4 + 4 i
A. maxP= 4 5
B. maxP= 7 5
C. maxP= 5 5
D. maxP= 6 5
Đáp án A
Cho số phức ![]() ,S(x;y) là điểm biểu diễn của z trên hệ trục tọa độ Oxy
,S(x;y) là điểm biểu diễn của z trên hệ trục tọa độ Oxy
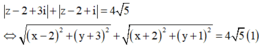
Lấy các điểm A(2;-3),B(-2;-1)
Phương trình ![]()
![]() Tập hợp các điểm S là đường elip (E) có tiêu điểm A(2;-3),B(-2;-1) và có độ dài trục lớn là
Tập hợp các điểm S là đường elip (E) có tiêu điểm A(2;-3),B(-2;-1) và có độ dài trục lớn là ![]()
Lấy M(4;-4).
Dễ dàng kiểm tra được 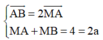
Suy ra, M là một đỉnh và nằm trên trục lớn của elip (E).
Gọi I là trung điểm AB
![]() I(0;-2) ,N là điểm đối xứng của M qua I.
I(0;-2) ,N là điểm đối xứng của M qua I.
Khi đó, với mọi điểm ![]()
![]() khi và chỉ khi S trùng N
khi và chỉ khi S trùng N
![]() khi và chỉ khi S
≡
N(-4;0)
khi và chỉ khi S
≡
N(-4;0)
![]() z=-4
z=-4
Cho số phức z thỏa mãn 3 + 2 i z + 2 - i 2 = 4 + i , tính z
A. z = 1
B. z = 0
C. z = 2
D. z = 2
Cho số phức z thỏa mãn (2+i)z=4-3i Tìm mô đun cua số phức w=iz +2\(\overline{z}\)
gọi z= a + bi \(\left(a,b\in R\right)\)
(2+i)(a+bi)=4-3i
\(\Leftrightarrow\) \(2a-b+\left(a+2b\right)i=4-3i\)
\(\Leftrightarrow\begin{cases}2a-b=4\\a+2b=-3\end{cases}\)
\(\Leftrightarrow\begin{cases}a=1\\b=-2\end{cases}\)
\(z=1-2i\)
w= i(1-2i) + 2( 1+ 2i) = 4 + 5i
Mình tưởng tìm moodun của một số \(\sqrt{a^2+b^2}\) chứ. @Nhók Lì Lợm