Cho tham số thực a. Biết phương trình e x - e - x = 2 cos a x có 5 nghiệm thực phân biệt. Hỏi phương trình e x - e - x = 2 cos a x + 4 có bao nhiêu nghiệm thực phân biệt?
A. 5.
B. 6.
C. 10.
D. 11.
Cho tham số thực a. Biết phương trình ex - e-x = 2 cosax có 5 nghiệm thực phân biệt. Hỏi phương trình ex - e-x = 2 cosax + 4 có bao nhiêu nghiệm thực phân biệt?
A. 5.
B. 6.
C. 10.
D. 11.
Chọn C.
Ta có
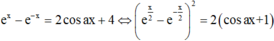
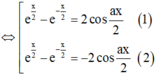
Giả sử x0 là nghiệm của phương trình ex - e-x = 2 cosax (*), thì x0 ≠ 0 và 2x0 là nghiệm của (1) và -2x0 là nghiệm của (2) hoặc ngược lại
Phương trình (*) có 5 nghiệm nên hai phương trình (1), (2) có 5 nghiệm phân biệt.
Vậy phương trình ex - e-x = 2 cosax + 4 có 10 nghiệm phân biệt.
Cho tham số thực a. Biết phương trình e x − e − x = 2 cos a x có 5 nghiệm thực phân biệt. Hỏi phương trình e x − e − x = 2 cos a x + 4 có bao nhiêu nghiệm thực phân biệt?
A. 5.
B. 6.
C. 10.
D. 11.
Cho phương trình log 2 ( x + a ) = 3 , với a là tham số thực. Biết phương trình có nghiệm x=2. Giá trị của a bằng
A. 1.
B. 10
C. 5
D. 6.
Có bao nhiêu giá trị nguyên của tham số m để phương trình
m + 3 . m + cos x 3 3 = cos x có nghiệm thực?
A. 2.
B. 7.
C. 5.
D. 3.
Có bao nhiêu giá trị nguyên của tham số m để phương trình sin 2 x + cos 2 x + | sin x + cos x | - cos 2 x + m - m = 0 có nghiệm thực?
A. 9
B. 2
C. 3
D. 5
Đáp án C
Sử dụng tính đơn điệu của hàm số, đánh giá số nghiệm của phương trình.
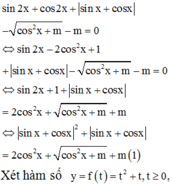
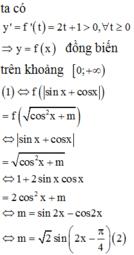

Vậy, có 3 giá trị nguyên của m thỏa mãn yêu cầu đề bài.
Cho phương trình 3 x = a . 3 x cos ( π x ) - 9 . Có bao nhiêu giá trị thực của tham số a thuộc đoạn [ -2018; 2018] để phương trình đã cho có đúng một nghiệm thực?
A. 1
B. 2018
C. 0
D. 2
e. Cho phương trình x² −2x+m=0 (x là ẩn số, m là tham số). Với giá trị nào của m thì phương trình có hai nghiệm x1, x2 thỏa mãn: 2(x1.x2) ²−x1=6+x2 Giải chi tiết giúo e ạ
\(x^2-2x+m=0\)
\(\Delta=b^2-4ac=\left(-2\right)^2-4m=4-4m\)
Để pt có 2 nghiệm \(x_1,x_2\) thì \(\Delta>0\Leftrightarrow4-4m>0\Leftrightarrow-4m>-4\Leftrightarrow m< 1\)
Theo Vi-ét, ta có : \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=2\\x_1x_2=\dfrac{c}{a}=m\end{matrix}\right.\)
Ta có : \(2\left(x_1x_2\right)^2-x_1=6+x_2\)
\(\Leftrightarrow2\left(x_1x_2\right)^2-x_1-x_2-6=0\)
\(\Leftrightarrow2\left(x_1x_2\right)^2-\left(x_1+x_2\right)-6=0\)
\(\Leftrightarrow2m^2-2-6=0\)
\(\Leftrightarrow2m^2=8\)
\(\Leftrightarrow m^2=4\)
\(\Leftrightarrow\left[{}\begin{matrix}m=2\left(ktm\right)\\m=-2\left(tm\right)\end{matrix}\right.\)
Vậy \(m=-2\) thì thỏa mãn đê bài.
Cho phương trình (m^2+1)x- 2m=0 (m là tham số).
a) Chứng minh phương trình là bậc nhất một ẩn với mọi giá trị của m.
b) Tìm m để nghiệm của phương trình đạt giá trị lớn nhất.
mnm giúp e với ạ, e cảm ơn nhìu nhìu
a) m2+1\(\ge\)1 \(\forall\)m, suy ra phương trình đã cho là phương trình bậc nhất một ẩn với mọi m.
b) Nghiệm của phương trình đã cho là x=\(\dfrac{2m}{m^2+1}\) (*).
Áp dụng BĐT Co-si cho hai số dương m2 và 1, ta có:
m2+1\(\ge\)2\(\sqrt{m^2.1}\)=2|m|.
Dấu "=" xảy ra khi và chỉ khi m2=1 \(\Rightarrow\) m=\(\pm\)1.
Với m=1, x=1.
Với m=-1, x=-1.
So sánh hai giá trị của x, ta kết luận: giá trị m cần tìm là m=1.
Tất cả các giá trị thực của tham số m để phương trình cos 2 x - 2 m - 1 cos x - m + 1 = 0 có đúng 2 nghiệm thuộc đoạn - π 2 ; π 2 là
A. - 1 ≤ m ≤ 0
B. 0 ≤ m ≤ 1
C. - 1 ≤ m ≤ 1
D. 0 ≤ m ≤ 1