Thể tích của khối lăng trụ tứ giác đều ABCD.A'B'C'D' có tất cả các cạnh bằng a là
![]()
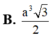
![]()
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Cho hình lăng trụ \(ABCD.A'B'C'D'\). Biết \(A'.ABCD\) là hình chóp đều có tất cả các cạnh đều bằng nhau và bằng \(a\). Tính theo \(a\) thể tích của khối lăng trụ \(ABCD.A'B'C'D'\) và thể tích của khối chóp \(A'.BB'C'C\).
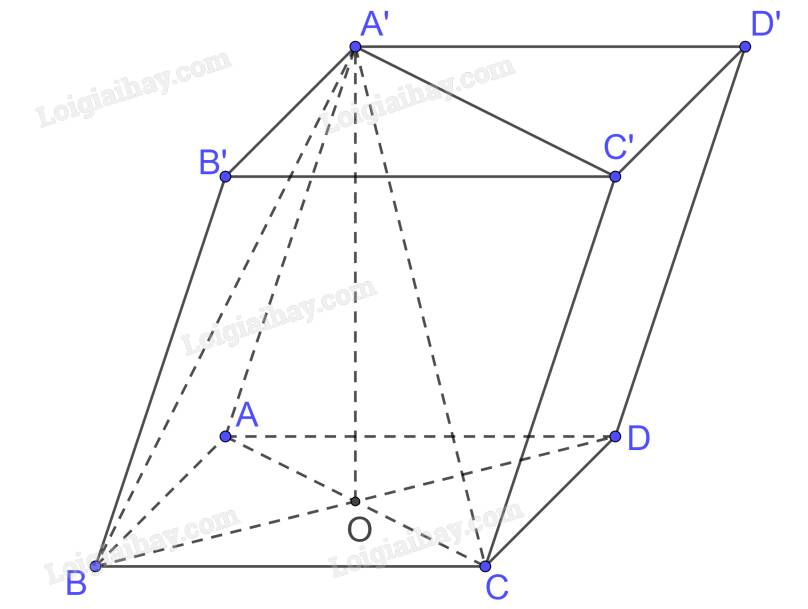
Gọi \(AC \cap BD = \left\{ O \right\}\) mà A’.ABCD là hình chóp đều nên \(A'O \bot \left( {ABCD} \right)\)
Xét tam giác ABC vuông tại B có \(AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \)
\( \Rightarrow OA = \frac{{AC}}{2} = \frac{{a\sqrt 2 }}{2}\)
Xét tam giác A’AO vuông tại O có
\(A'O = \sqrt {A{{A'}^2} - A{O^2}} = \sqrt {{a^2} - {{\left( {\frac{{a\sqrt 2 }}{2}} \right)}^2}} = \frac{{a\sqrt 2 }}{2}\)
\({S_{ABCD}} = {a^2}\)
Vậy khối lăng trụ có thể tích \(V = \frac{1}{3}A'O.{S_{ABCD}} = \frac{1}{3}.\frac{{a\sqrt 2 }}{2}.{a^2} = \frac{{{a^3}\sqrt 2 }}{6}\)
Nếu hình lăng trụ \(ABCD.A'B'C'D'\) xoay lại thành hình lăng trụ AA’D’D.BB’C’C thì thể tích không thay đổi do đó thể tích hình chóp \(A'.BB'C'C\) bằng một phần 3 thể tích hình lăng trụ AA’D’D.BB’C’C vì chung đáy và chung chiều cao kẻ từ A’ xuống đáy BB’C’C.
Thể tích khối chóp là \({V_{A'.BB'C'C}} = \frac{1}{3}.\frac{{{a^3}\sqrt 2 }}{6} = \frac{{{a^3}\sqrt 2 }}{{18}}\)
Thể tích của khối lăng trụ tứ giác đều ABCDA'B'C'D' có tất cả các cạnh bằng a là
A. 3 a 3
B. a 3 3 2
C. a 3
D. a 3 3 4
Đáp án C
Thể tích khối lăng trụ cần tính là: V = A A ' . S A B C D = a . a 2 = a 3 .
Cho lăng trụ tứ giác đều có tất cả các cạnh bằng nhau và biết tổng diện tích các mặt của lăng trụ bằng 296cm . Tính thể tích khối lăng trụ.
A. 128 c m 2
B. 64 c m 2
C. 32 c m 2
D. 60 c m 2
Đáp án B
Hình lăng trụ tứ giác đều có tất cả các cạnh bằng nhau là hình lập phương.
Gọi a là độ dài một cạch thì tổng diện tích các mặt S = 6 a 2 => a = 4.
=> thể tích lăng trụ là V = a 3 = 4 3 = 64
Cho lăng trụ tứ giác đều có tất cả các cạnh bằng nhau và biết tổng diện tích các mặt của lăng trụ bằng 296cm . Tính thể tích khối lăng trụ
A.128 c m 2 .
B.64 c m 2 .
C.32 c m 2 .
D.60 c m 2 .
Đáp án B
Hình lăng trụ tứ giác đều có tất cả các cạnh bằng nhau là hình lập phương.
Gọi a là độ dài một cạch thì tổng diện tích các mặt S = 6 a 2 = 96 ⇒ a = 4 c m
thể tích lăng trụ là V = a 3 = 4 3 = 64 c m 3
Cho lăng trụ tứ giác đều ABCD.A'B'C'D' có cạnh đáy bằng a và cạnh bên bằng 9a. Tính thể tích khối lăng trụ đó.
A. 9a3
B. 36a3
C. 12a3
D. 3a3
Đáp án A
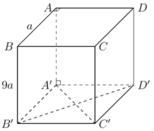
Ta có ABCD.A'B'C'D' là lăng trụ tứ giác đều nên có đáy là hình vuông và cạnh bên vuông góc với đáy.
Suy ra VABCD.A'B'C'D' = SABCD. AA' = a2. 9a = 9a3.
Cho lăng trụ tứ giác đều A B C D . A ' B ' C ' D ' có cạnh đáy bằng 2a. Khoảng cách từ A đến mặt phẳng ( A ' B C ) bằng a 3 . Thể tích khối lăng trụ là.

A. 8 a 3 3
B. 4 a 3 3
C. 8 3 a 3 3
D. 3 a 3 3
Đáp án A.
Từ A dựng A H ⊥ A ' B ( H ∈ A ' B )
⇒ A H = a 3
1 A H 2 = 1 A A ' 2 + 1 A B 2
⇒ 1 A A ' 2 = 1 3 a 2 - 1 4 a 2 = 1 12 a 2
⇒ A A ' = 2 a 3 ⇒ V = 8 a 3 3
Cho lăng trụ tứ giác đều ABCD.A'B'C'D' có cạnh đáy bằng 2a. Khoảng cách từ A đến mặt phẳng (A'BC) bằng a 3 . Thể tích khối lăng trụ là.
A. 8 a 3 3
B. 4 a 3 3
C. 8 3 a 3 3
D. 3 a 3 3
Cho lăng trụ tứ giác đều ABCD.A'B'C'D' có cạnh đáy bằng 2a. Khoảng cách từ A đến mặt phẳng (A'BC) bằng a 3 . Thể tích khối lăng trụ là.
![]()
![]()
![]()
![]()
Cho lăng trụ tứ giác đều A B C D . A ' B ' C ' D ' có cạnh đáy bằng 2a. Khoảng cách từ A đến mặt phẳng (A'BC) bằng a 3 . Thể tích khối lăng trụ là
A. 8 a 3 3
B. 4 a 3 3
C. 8 3 a 3 3
D. 3 a 3 3