Xét các số thực a, b thỏa mãn a> b > 1. Tìm giá trị nhỏ nhất của biểu thức P = log a b 2 ( a 2 ) + 3 log b a b
A. P m i n = 19
B. P m i n = 13
C. P m i n = 14
D. P m i n = 15
Xét các số thực a, b thỏa mãn a > b > 1. Tìm giá trị nhỏ nhất của biểu thức P = log a b 2 a 2 + 3 log b a b .
A. P min = 19.
B. P min = 13.
C. P min = 14.
D. P min = 15.
Xét các số thực a, b thỏa mãn a > b > 1 . Tìm giá trị nhỏ nhất của biểu thức P = log a b 2 a 2 + 3 log b a b
A. P m i n = 19
B. P m i n = 13
C. P m i n = 14
D. P m i n = 15
Xét các số thực a; b thỏa mãn a> b> 1 . Tìm giá trị nhỏ nhất Pmin của biểu thức P = log 2 a b a 2 + 3 log b a b
A. 19
B. 13
C. 14
D. 15
Ta có:
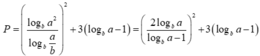
Đặt t= logba-1 > logbb -1=0 ,
khi đó:
P = 2 t + 2 t 2 + 3 t = f ( t ) f ' t = 2 . 2 t + 2 t . - 2 t 2 + 3 = 3 t 3 - 8 ( t + 1 ) t 3
F’ (t) =0 khi 3t3-8( t+1) =0 hay t= 2.
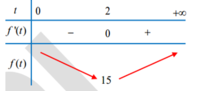
Suy ra Pmin =f(2) =15
Chọn D.
Xét các số thực a; b thỏa mãn a > b > 1 . Tìm giá trị nhỏ nhất của P của biểu thức P = log a b 2 a 2 + 3 log b a b
A. 19.
B. 13.
C. 14.
D. 15.
Chọn D.
Ta có:
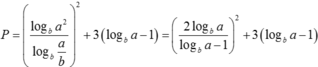
Đặt t = logba – 1 > logbb – 1 = 0; khi đó:
![]()
Ta có: ![]()
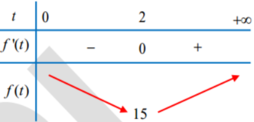
Và f’(t) = 0 khi 3t3 - 8( t + 1) = 0 hay t = 2.
Suy ra Pmin = f(2) = 15
Xét các số thực a; b thỏa mãn a > b > 1 Tìm giá trị nhỏ nhất Pmin của biểu thức P = log a b 2 a 2 + 3 log b a b
A.19
B.13
C.14
D.15
Xét các số thực âm a,b,c thay đổi thỏa mãn điều kiện 4(ab+bc+ac)=9abc+1 tìm giá trị nhỏ nhất của biểu thức P=a+b+c
Ủa số thực âm hay không âm vậy em?
Đặt \(a+b+c=p\) ; \(ab+bc+ca=q\) ; \(abc=r\)
\(\Rightarrow p^2\ge3q\)
Từ giả thiết: \(4q=9r+1\)
Áp dụng BĐT Schur bậc 3: \(r\ge\dfrac{4pq-p^3}{9}\)
\(\Rightarrow4q\ge4pq-p^3+1\Leftrightarrow p^3-1+4q-4pq\ge0\)
\(\Leftrightarrow\left(p-1\right)\left(p^2+p+1-4q\right)\ge0\)
Nếu \(p< 1\Rightarrow p^2+p+1-4q\le0\)
Mà \(p< 1\Rightarrow1>p^2\Rightarrow0\ge p^2+p+1-4q>p^2+p+p^2-4q\)
\(\Rightarrow2\left(p^2-2q\right)+p< 0\) (vô lý do \(p^2\ge3q\ge2q\))
\(\Rightarrow p\ge1\)
Vậy \(P_{min}=1\) khi \(a=b=c=\dfrac{1}{3}\) hoặc \(\left(a;b;c\right)=\left(\dfrac{1}{2};\dfrac{1}{2};0\right)\) và các hoán vị
Xét các số thực a, b thỏa mãn b>1 và a ≤ b < a Biểu thức P = log a b a + 2 log b a b đạt giá trị nhỏ nhất khi
A . a = b 2
B . a 2 = b 3
C . a 3 = b 2
D . a 2 = b
xét hai số thực dương a,b thỏa mãn \(a^2\)+\(b^2\)=2 tìm giá trị nhỏ nhất của biểu thức P=\(\dfrac{a^2}{b+1}\)+\(\dfrac{b^2}{a+1}\)
Ta thấy \(ab\le\dfrac{a^2+b^2}{2}=1\) và \(a+b\le\sqrt{2\left(a^2+b^2\right)}=2\). Áp dụng BĐT B.C.S, ta được \(P=\dfrac{a^4}{ba^2+a^2}+\dfrac{b^4}{ab^2+b^2}\) \(\ge\dfrac{\left(a^2+b^2\right)^2}{ba^2+ab^2+a^2+b^2}=\dfrac{2^2}{ab\left(a+b\right)+2}\ge\dfrac{4}{1.2+2}=1\)
ĐTXR \(\Leftrightarrow a=b=1\)
Vậy GTNN của P là 1 khi \(a=b=1\)
Xét các số thực a, b thỏa mãn 1 4 < b < a < 1 Biểu thức P = log a ( b - 1 4 ) - log a b b đạt giá trị nhỏ nhất khi
A. log a b = 1 3
B. log a b = 2 3
C. log a b = 3 2
D. log a b = 3