Tìm tất cả các giá trị của a để bất phương trình sau nghiệm đúng với mọi x.
a . 9 x + a - 1 3 x + 2 + a - 1 > 0
A. a > 1
B. a ≥ 1
C. a < 1
D. a ≤ 1
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Tìm tất cả các giá trị của m để bất phương trình sau nghiệm đúng với mọi x
\(m.9^x+\left(m-1\right)3^{x+2}+m-1>0\)
Đặt \(t=3^x,t>0\)
Bất phương trình trở thành :
\(m.t^2+9\left(m-1\right)t+m-1>0\)
\(\Leftrightarrow m\left(t^2+9t+1\right)>9t+1\)
\(\Leftrightarrow m>\frac{9t+1}{t^2+9t+1}\)
Bất phương trình đã cho nghiệm đúng với mọi x khi và chỉ khi :
\(m>max_{t>0}\frac{9t+1}{t^2+9t+1}\)
Xét hàm số \(f\left(t\right)=\frac{9t+1}{t^2+9t+1};t>0\)
Ta có : \(f'\left(t\right)=\frac{-9t-2}{\left(t^2+9t+1\right)^2}< 0,t>0\)
đây là hàm nghịch biến suy ra \(f\left(t\right)< f\left(0\right)=1\)
Do đó : \(\frac{9t+1}{t^2+9t+1}< 0,t>0\) nên các giá trị cần tìm là \(m\ge1\)
Tìm tất cả các giá trị thực của tham số m để bất phương trình 4 l o g 2 x 2 + log 2 x + m ≥ 0 nghiệm đúng với mọi giá trị x ∈ 1 ; 64
A. m ≤ 0
B. m ≥ 0
C. m < 0
D. m > 0
Bài 1. Tìm m để f (x)=mx^2 -2(m-1)x+4m-1 luôn dương Bài 2 tìm tất cả các giá trị của tham số m để bất phương trình sau có nghiệm đúng với mọi a.5x^2-x+m>0 b.m(m+2)x^2+2mx+2>0
Tìm tất cả các giá trị của tham số m để bất phương trình( m - 1) x^2-2x + m + 1> 0 nghiệm đúng với mọi x> 0
Có tất cả bao nhiêu giá trị nguyên của a để bất phương trình 2 log 1 2 a - 3 + 2 x . log 1 2 a - x 2 < 0 nghiệm đúng với mọi x.
A. 5
B. 6
C. 7
D. 8
Chọn C.
Bất phương trình
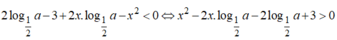
Đặt , 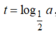 khi đó bất phương trình trở thành x2-2tx-2t+3> 0 (*)
khi đó bất phương trình trở thành x2-2tx-2t+3> 0 (*)
Bất phương trình (*) nghiệm đúng với mọi x khi và chỉ khi
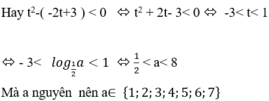
Vậy có tất cả 7 giá trị nguyên của a thỏa mãn yêu cầu bài toán.
Tìm tất cả các giá trị thực của tham số m để bất phương trình 2 x + 3 + 5 - 2 x ≤ m nghiệm đúng với mọi x ∈ - ∞ ; log 2 5
A. m ≥ 4
B. m < 4
C. m ≥ 2 2
D. m < 2 2
Tìm tất cả các giá trị thực của tham số m để bất phương trình x 2 + 3 x + 3 x + 1 ≥ m nghiệm đúng với mọi x ∈ 0 ; 1
A. m ≥ 3
B. m ≤ 7 2
C. m ≥ 7 2
D. m ≤ 3
Đáp án D
Để bất phương trình m ≤ f x = x 2 + 3 x + 3 x + 1 ; ∀ x ∈ 0 ; 1 ⇔ m ≤ min 0 ; 1 f x
Xét hàm số f x = x 2 + 3 x + 3 x + 1 trên 0 ; 1 ⇒ min 0 ; 1 f x = 3 . Vậy m ≤ 3
Cho phương trình m . 9 x - 2 m + 1 6 x + m . 4 x ≤ 0 . Tìm tất cả các giá trị của tham số m để bất phương trình nghiệm đúng với mọi x thuộc (0;1]
A. m ≥ - 6
B. - 6 ≤ m ≤ 4
C. m ≥ - 4
D. m ≤ - 6
Bất phương trình đã cho 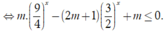
Đặt  Bất phương trình trở thành
Bất phương trình trở thành ![]()
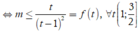
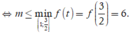
Chọn D.
Cho bất phương trình m . 3 x + 1 + ( 3 m + 2 ) ( 4 - 7 ) x + ( 4 + 7 ) x > 0
với m là tham số. Tìm tất cả các giá trị của tham số m để bất phương trình đã cho nghiệm đúng với mọi x ∈ ( - ∞ , 0 )
A. m > 2 + 2 3 3
B. m > 2 - 2 3 3
C. m ≥ 2 - 2 3 3
D. m ≥ - 2 - 2 3 3