Hệ số của x 7 trong khai triển nhị thức ( 1 + x ) 12 bằng
A. 820.
B. 220.
C. 792.
D. 210.
Cho nhị thức x + 1 x n , x ≠ 0 trong tổng số các hệ số của khai triển nhị thức đó là 1024. Khi đó số hạng không chứa x trong khai triển nhị thức đã cho bằng
A. 252
B. 125
C. -252
D. 525
Hệ số của x8 trong khai triển nhị thức (x+ 1/x)20 là
Lời giải:
Theo khai triển Newton:
\((x+\frac{1}{x})^{20}=\sum\limits_{k=0}^{20}C^k_{20}x^k(x^{-1})^{20-k}=\sum\limits_{k=0}^{20}C^k_{20}x^{2k-20}\)
$2k-20=8\Leftrightarrow k=14$
Hệ số của $x^8$ là: $C^{14}_{20}$
Hệ số của x 7 trong khai triển nhị thức ( 1 + x ) 12 bằng
A. 820
B. 220
C. 792
D. 210
Chọn C
Ta có 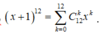 . Hệ số của
x
7
ứng với k = 7 là
C
12
7
=
792
.
. Hệ số của
x
7
ứng với k = 7 là
C
12
7
=
792
.
Tìm hệ số lớn nhất trong khai triển nhị thức Newton của P ( x ) = 1 + 2 x 12
A. 126700.
B. 126730.
C. 126720.
D. 126710.
Đáp án C
Ta có P ( x ) = 1 + 2 x 12 = ∑ k = 0 12 C 12 k 1 12 - k = ∑ k = 0 12 C 12 k 2 k x k .
Gọi a k = C 12 K 2 K , 0 ≤ k ≤ 12 , k ∈ ℕ là hệ số lớn nhất trong khai triển.
Suy ra a k ≥ a k + 1 a k ≥ a k - 1 ⇔ c 12 k 2 k ≥ c 12 k + 1 2 k + 1 c 12 k 2 k ≥ c 12 k - 1 2 k - 1
⇔ 12 ! 12 - k ! k ! . 2 k ≥ 12 ! 11 - k ! k + 1 ! . 2 k + 1 12 ! 12 - k ! k ! . 2 k ≥ 12 ! 13 - k ! k + 1 ! . 2 k - 1 ⇔ 1 12 - k ≥ 2 k + 1 1 k ≥ 1 2 13 - k
Vậy hệ số lớn nhất trong khai triển đã cho là a 8 = 2 8 c 12 8 = 126720 .
Tổng các hệ số nhị thức Niu – tơn trong khai triển (1+x)3n bằng 64. Số hạng không chứa x trong khai triển 2 n x + 1 2 n x 2 3 n là:
A. 360
B. 210
C. 250
D. 240
Ta có: 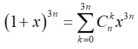
Chọn x=1. Ta có tổng hệ số bằng: ![]()
Lại có: 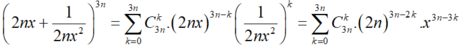
Số hạng không chứa x suy ra ![]()
Do đó số hạng không chứa x là: ![]()
Chọn D.
Trong khai triển nhị thức x + 1 x n , x ≠ 0 , hệ số của số hạng thứ 3 lớn hơn hệ số của số hạng thứ 2 là 35. Tìm số hạng không chứa x trong khai triển nói trên.
A. 225
B. 252
C. 522
D. 525
Trong khai triển nhị thức x + 1 x n , x ≠ 0 hệ số của số hạng thứ 3 lớn hơn hệ số của số hạng thứ 2 là 35. Tìm số hạng không chứa x trong khai triển nói trên.
A. 225
B. 252
C. 522
D. 525
Trong khai triển nhị thức ( x + 1 x ) n hệ số của số hạng thứ 3 lớn hơn hệ số của số hạng thứ 2 là 35. Tìm số hạng không chứa x trong khai triển nói trên.
A. 225
B. 252
C. 522
D. 525
Tổng các hệ số nhị thức Niu – tơn trong khai triển ( 1 + x ) 3 n bằng 64. Số hạng không chứa x trong khai triển ( 2 n x + 1 2 n x 2 ) 3 n là
A. 360
B. 210
C. 250
D. 240