Chủ đề / Chương

Bài học

Hãy tham gia nhóm Học sinh Hoc24OLM
PB
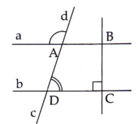
Cho hình vẽ bên dưới biết a A d ^ 110 o , A D C ^ 70 o  và B C ⊥ b . Số đo A B C ^  là:A.  70 ° B.  90 ° C. ...
Đọc tiếp
Lớp 7 Toán
Những câu hỏi liên quan
PB
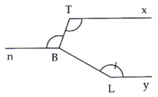
Cho hình vẽ bên, biết hai tia Tx//Ly, x T B ^ T B n ^   110 ° và B L y ^   150 ° .Tính số đo góc  T B L ^ A.  150 ° ; B. ...
Đọc tiếp
Xem chi tiết
Lớp 7 Toán

Khách
 
CT
5 tháng 7 2017 lúc 12:07

Chọn D

Bình luận (0)
PB

Cho hình vẽ bên có a // b. Số đo của B O N ^  là:

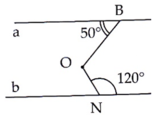
A. 100 ° ;

B. 110 ° ;

C. 80 ° ;

D. 120 °

Xem chi tiết
Lớp 7 Toán

Khách
 
CT
18 tháng 1 2019 lúc 15:33

Chọn B

Bình luận (0)
PB

Cho hình vẽ bên. Số đo của x là:

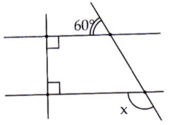
A.  100 ° ;

B.  110 ° ;

C.  130 ° ;

D.  120 °

Xem chi tiết
Lớp 7 Toán

Khách
 
CT
5 tháng 3 2018 lúc 13:42

Chọn D

Bình luận (0)
BC
Cho hình vẽ: a c/m AB //CDb c/m AD//BCc tính góc C1;C2;C3 A B C D 1 2 3 1 1 1 110 110 70 O O O
Đọc tiếp
Xem chi tiết
Lớp 7 Toán

Khách
 
DN
5 tháng 7 2021 lúc 17:28

do đọ dài

 

Bình luận (0)
JP
5 tháng 7 2021 lúc 18:32

ơ sao góc A 1 lại bằng 110 độ nhờ

 

 

Bình luận (1)
NN
Cho hình vẽ, biết C 110 1  0 .a, Chứng minh AC // BD.b/ Tính số đo của D1 và D2 . A B C D 1 1 2
Đọc tiếp
Xem chi tiết
Lớp 7 Toán Bài 4: Hai đường thẳng song song

Khách
 
NT
24 tháng 12 2023 lúc 19:17

a: Ta có: AC\(\perp\)AB

BD\(\perp\)AB

Do đó: AC//BD

b: bạn vẽ lại hình nha bạn

Bình luận (0)
N7
Câu 55 : Cho hình vẽ sau , biết AD // BC . Tính A G B D C 110độ 140độ A .  ^{ } 110 độ ^{ }                         B .    140độ        C .  120độ                  D . 130độ
Đọc tiếp
Xem chi tiết
Lớp 7 Toán

Khách
 
H24
20 tháng 11 2021 lúc 16:05

A

Bình luận (0)
H24

Trong hình bên biết: ˆBAD= 110°, ˆABC = 70°, ˆBCD = 90°BAD^= 110°, ABC^ = 70°, BC^D = 90°.

Chứng minh hai đường thẳng a và d vuông góc với nhau.

Xem chi tiết
Lớp 7 Toán

Khách
 
H24
21 tháng 10 2021 lúc 16:43

Ta có: \(\widehat{BAD}+\widehat{ABC}=110^o+70^o=180^o\)

Mà 2 góc này là 2 góc trong cùng phía ⇒a//b

a//b, b⊥d⇒a⊥d

Bình luận (0)
NC
21 tháng 10 2021 lúc 16:44

Ta có \(\widehat{BAD}\) + \(\widehat{ABC}\) = 180° => a // b

Mà \(\widehat{BCD}\) = 90°=>d ⊥ b. Do đó d  ⊥ a

Bình luận (0)
N7
Câu 43 : Cho hình vẽ dưới đây , biết AB // CD . Số đo của góc C là : A B C D 120độ A .50^{ }o                             B .60o                              C . 80o                       D .120o
Đọc tiếp
Xem chi tiết
Lớp 7 Toán

Khách
 
H24
21 tháng 11 2021 lúc 14:23

B

Bình luận (0)
SK
21 tháng 11 2021 lúc 14:23

B

Bình luận (0)
OY
21 tháng 11 2021 lúc 14:24

B

Bình luận (0)
Xem thêm câu trả lời
NH
Cho hình vẽ sau,biết rằng EB=ED.Chứng minh rằng: a, tam giác EAB=tam giác ECD b,AB=CD c, tam giác ABC=tam giác CDA d,AD//BCGiúp em dớiHình vẽ để bên dưới
Xem chi tiết
Lớp 7 Toán

Khách
 
DH
7 tháng 3 2021 lúc 19:20

Xét tam giác AEB và tam giác CED có 

góc BAE = góc DCE = 90 độ

BE = CE

góc BEA = góc DEC (đối đỉnh)

=> tam giác AEB = tam giác CED (ch-gn)

b) Có tam giác AEB = tam giác CED => AB = CD

c) Xét tam giác ABC và tam giác CDA có 

góc BAC = góc DCA = 90 độ

AB = CD

AC chung

=> tam giác ABC = tam giác CDA (c.g.c)

d) ta có tam giác ABC = tam giác CDA => góc BCA = góc DAC (2 góc tương ứng )

mà 2 góc ở vị trí so le trong => AD // BC

Bình luận (0)
NT
7 tháng 3 2021 lúc 19:18

a) Xét ΔEAB vuông tại A và ΔECD vuông tại C có 

EB=ED(gt)

\(\widehat{AEB}=\widehat{CED}\)(hai góc đối đỉnh)

Do đó: ΔEAB=ΔECD(cạnh huyền-góc nhọn)

Bình luận (0)
NH
7 tháng 3 2021 lúc 19:16

undefined

Bình luận (0)

Khoá học trên OLM (olm.vn)