Có bao nhiêu số phức z thỏa mãn 2 z + z ¯ + z - z ¯ - 2 i = 8 và z = 2
A. 2
B. 0
C. 4
D. 6
Cho số phức z thỏa mãn ( 1 - 3i) z là số thực và ![]() . Hỏi có bao nhiêu số phức z thỏa mãn
. Hỏi có bao nhiêu số phức z thỏa mãn
A. 1
B. 2
C. 3
D. 4
Chọn B.
Gọi số phức cần tìm là z = a + bi.
Ta có ( 1 - 3i) z = ( 1 - 3i) ( a + bi)
= a + 3b - 3ai + bi = a + 3b + ( b - 3a) i
+ Do ( 1 - 3i) z là số thực nên b - 3a = 0 hay b = 3a
+ ta có ![]() ⇔|a – 2 + (-b + 5)i| = 1
⇔|a – 2 + (-b + 5)i| = 1
Hay ( a - 2) 2 + ( 5 - 3a) 2 = 1
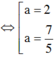 (thỏa mãn)
(thỏa mãn)
Vậy có hai số phức z thỏa mãn là z = 2 + 6i và z = 7/5 + 21/5i
Có bao nhiêu số phức z thỏa mãn z 2 = | z | 2 + z ¯
A. 4.
B. 2.
C. 3.
D. 1.
Đáp án C.
Giả sử ![]()
![]()
![]()

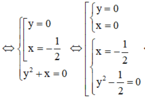
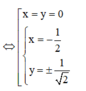
Do đó có 3 số phức z thỏa mãn bài toán.
Có bao nhiêu số phức z thỏa mãn 2 z + z ¯ + z - z ¯ - 2 i = 8 và z = 2 ?
A. 2
B. 0
C. 4
D. 6
Đặt z=a+bi ta có z = 2 ⇔ a 2 + b 2 = 4 ( 1 )
Và ![]()
![]()
Biểu diễn (1), (2) trên cùng hệ trục toạ độ:
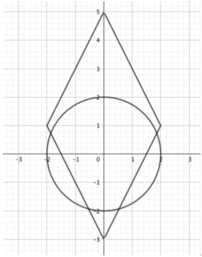
Chúng cắt nhau tại 4 điểm phân biệt, tức có 4 số phức thoả mãn.
Chọn đáp án C.
*Chú ý cách giải trên là nhanh nhất, các em có thể xét các trường hợp của trị tuyệt đối và giải hệ phương trình.
*Hình thoi trên hình vẽ được vẽ nhanh bằng cách đi tìm các đỉnh của nó, đó là giải các hệ phương trình
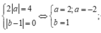
![]()
Chọn đáp án C.
Có bao nhiêu số phức z thỏa mãn: z 2 + z ¯ 2 = 26 và z + z ¯ = 6
A. 2.
B. 3.
C. 2.
D. 1.
Chọn A.
Đặt z = x + iy (x, y ∈ R), ta có ![]()
Ta có:
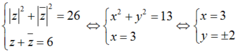
⇒ có 2 số phức thỏa yêu cầu đề bài.
Có tất cả bao nhiêu số phức z thỏa mãn z + z + z - z = 4 và z - 2 - 2 i = 3 2
A. 7
B. 3
C. 2
D. 5
Có bao nhiêu số phức z thỏa mãn điều kiện z . z ¯ + z = 2 và |z| = 2?
A. 1
B. 2
C. 3
D. 4
Có bao nhiêu số phức z thỏa mãn điều kiện z . z ¯ + z = 2 và z = 2
A. 2
B. 3
C. 1
D. 4
Có bao nhiêu số phức z thỏa mãn điều kiện z z ¯ + z = 2 và z = 2
A. 4.
B. 3
C. 2
D. 1
Đáp án D
Ta có z . z ¯ = z 2 ⇒ z . z ¯ + z = 2 ⇔ z 2 + z = 2 ⇔ z + 4 = 2 (do z = 2 )
Đặt z = x + y i , x ; y ∈ ℝ
Ta có
z + 4 = 2 z = 2 ⇔ x + 4 2 + y 2 = 4 x 2 + y 2 = 2 ⇔ x + 4 − x x + 4 + x = 0 x 2 + y 2 = 4 ⇔ x = − 2 y = 0
Vậy có duy nhất một giá trị z = − 2 thảo mãn yêu cầu đề bài
Có bao nhiêu số phức z thỏa mãn điều kiện z z ¯ + z = 2 và z = 2 ?
A. 4
B. 3
C. 2
D. 1