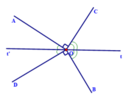
Cho hình vẽ bên:
Chứng tỏ Ot và Ot’ là hai tia đối nhau.
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
cho hai đường thẳng xx' và yy' giao nhau tại điểm O. Gọi Ot là tia phân giác của góc xOy;vẽ tia Ot' là tia phân giác của góc x'Oy'. hãy chứng tỏ Ot và Ot' là 2 tia đối nhau (vẽ hình mik mới cho điểm)
Cho hai đường thẳng x, y cắt nhau tại điểm O. Vẽ tia Ot là tia phân giác của góc NOy và tia Ot' là tia phân giác của góc xOM. Hãy chứng tỏ Ot và Ot' là hai tia đối nhau.
Cho hai đường thẳng xx' và yy' giao nhau tại O. Gọi Ot là tia phân giác của góc xOy; vẽ tia Ot' là tia phân giác của góc x'Oy'. Hãy chứng tỏ Ot' là tia đối của Ot.
Cho hai đường thẳng xx' và yy' giao nhau tại O, Gọi Ot là tia phân giác của góc xOy, vẽ tia phân giác của góc x'Oy', Hyax chứng tỏ Ot' là tia đối của tia Ot
ta có: xx' cắt yy' tại O
=> góc xOy = góc x'Oy' ( đối đỉnh)
=> góc xOy/2 = góc x'Oy'/2
mà góc O1 = góc xOy/2 ( định lí tia phân giác)
góc O2 = góc xOy/2 ( định lí tia phân giác)
=> góc O1 = góc O2
mà góc O1 = góc xOy/2 => góc O1. 2 = góc xOy
mà góc xOy + góc xOy' = 180 độ
=> góc O1 .2 + góc xOy' = 180 độ
góc O1 + góc O1 + góc xOy' = 180 độ
=> góc O1 + góc O2 + góc xOy' = 180 độ ( góc O1 = góc O2)
=> Ot' là tia đối của tia Ot ( định lí)
Ví dụ 7. Trên đường thẳng t’t lấy điểm O. Trên hai nửa mặt phẳng đối nhau bờ t’t ta vẽ hai tia Ox và Oy. Chứng tỏ rằng có ít nhất một trong hai tia Ot, Ot’ nằm giữa hai tia Ox và Oy.
Ví dụ 8. Cho tia Ot nằm giữa, hai tia Oa, Ob không đối nhau; tia Om nằm giữa hai tia Oa, Ot; tia On nằm giữa hai tia Ob, Ot. Chứng tỏ rằng tia Ot nằm giữa hai tia Om, On.
Ví dụ 7 :
Lấy A trên tia Ox, B trên tia Oy. Hai điểm A, B thuộc hai nửa mặt phẳng đối nhau bờ t’t nên đường thẳng t’t cắt
đoạn thẳng AB tại một điểm M nằm giữa A và B. Do đó có ít nhất một trong hai tia Ot, Ot’ cắt đoạn thẳng AB tại M,
tức là có ít nhất một trong hai tia ot, ot’ nằm giữa hai tia Ox, Oy.
Ví dụ 8 :
Lấy điểm A trên tia Oa, điểm B trên tia Ob (A và B khác điểm O). Tia Ot nằm giữa hai tia Oa,
Ob nên cắt đoạn thẳng AB tại điểm c nằm giữa A và B. Tương tự, tia Om cắt đoạn thẳng AC tại điểm M nằm giữa A
và C; tia On cắt đoạn thẳng BC tại điểm N nằm giữa B và C. Từ đó suy ra điểm c nằm giữa hai điểm M và N, do đó
tia Ot nằm giữa hai tia Om và On.
Thanks bạn nhìu
1.Cho 2 góc kề bù xOy và yOz. Ot là tia phân giác của xOy, vẽ Ot' vuông góc với Ot(Ot' và Ot thuộc cùng 1 nửa mặt phẳng bơ). Chứng tỏ Ot' là tia phân giác của yOz.
2.Chứng tỏ:2 tia phân giác của 2 góc đối đỉnh là 2 tia đối nhau.
Cho hai đường thẳng xy và x’y’ cắt nhau tại O .vẽ tia Oz là TPG của góc x’Oy và Ot là TPG của góc xOy’
Chứng tỏ xOt= yOz
Chứng tỏ Oz và Ot đối nhau
Hai đường thẳng AB cắt nhau tại O sao cho góc AOC = 60o
a, Tính số đo các góc còn lại
b, Vẽ tia Ot là tia phân giác của góc AOC và vẽ tia Ot' là tia đối của tia Ot . Chứng tỏ rằng tia Ot là tia phân giác của góc BOD
Vẽ hình nx ạ
Cho hai đường thẳng AB và CD cắt nhau tại O sao cho AÔC=60 độ.
a) Tính số đo các góc còn lại
b) Vẽ tia Ot là tia phân giác của góc AOC và Ot' là tia đối của tia Ot. Chứng tỏ Ot' là tia phân giác của góc BOD
( Các bạn vẽ hình giúp mình nha,nhưng vẽ được không bắt buộc, chúc các bạn học tốt)
a) \(\widehat{DOB}=\widehat{AOC}=60^o\) (đối đỉnh)
Ta có : \(\widehat{AOC}+\widehat{BOC}=180^o\) (kề bù)
=> \(\widehat{BOC}=180^o-60^o=120^o\)
\(\widehat{AOD}=\widehat{BOC}=120^o\) (đối đỉnh)
b) Ot là tia p/g của góc AOC nên \(\widehat{tOc}=\frac{1}{2}\widehat{AOC}=30^o\)
Ta có : \(\widehat{tOC}+\widehat{BOC}+\widehat{t'OB}=180^o\) (kề bù)
=> \(30^o+120^o+\widehat{t'OB}=180^o\)
=> \(\widehat{t'OB}=30^o=\frac{1}{2}.60^o=\frac{1}{2}\widehat{BOD}\)
=> Ot' là tia p/g của góc BOD