Xét quan hệ giữa hai góc trong mỗi biểu thức rồi tính: sin 32 ° c o s 58 °
PB
Những câu hỏi liên quan
Xét quan hệ giữa hai góc trong mỗi biểu thức rồi tính: tg 76 ° – cotg 14 °
Ta có: 76 ° + 14 ° = 90 °
Suy ra: tg 76 ° = cotg 14 ° . Vậy tg 76 ° – cotg 14 ° = 0
Đúng 0
Bình luận (0)
xét quan hệ giữa hai góc trong mỗi biểu thức rồi tính
sin215 + sin235 + sin255 + sin275
\(\sin^215^0+\sin^235^0+\sin^255^0+\sin^275^0\)
=1+1
=2
Đúng 0
Bình luận (0)
Xét quan hệ giữa hai góc vuông trong mỗi biểu thức rồi tính:
a) \(\frac{sin32^o}{cos58^0}\)
b) tg76\(^o\) - cotg14\(^o\)
a: \(32^0+58^0=90^0\)
nên \(\sin32^0=\cos58^0\)
\(\Leftrightarrow\dfrac{\sin32^0}{\cos58^0}=1\)
b: \(76^0+14^0=90^0\)
nên \(\tan76^0=\cot14^0\)
\(\Leftrightarrow\tan76^0-\cot14^0=0\)
Đúng 0
Bình luận (0)
Xét quan hệ giữa hai góc vuông hai góc trong mỗi biểu thức ròi tính:
a) \(\frac{sin32^o}{cos58^o}\)
b) tg76\(^o\) - cotg14\(^o\)
Xét quan hệ giữa hai góc trong mỗi biểu thức rồi tính :
a) \(\dfrac{\sin32^0}{\cos58^0}\)
b) \(tg76^0-cotg14^0\)
a: \(\dfrac{\sin32^0}{\cos58^0}=\dfrac{\sin32^0}{\sin32^0}=1\)
b: \(\tan76^0-\cot14^0=\tan76^0-\tan76^0=0\)
Đúng 0
Bình luận (0)
Xét quan hệ giữa hai góc trong mỗi biểu thức rôi tính:
a) \(\frac{sin32^o}{cos58^o}\)
b) tg76\(^o\) - cotg14\(^o\)
Nêu nhận xét về vị trí của hai điểm M, M’ đối với trục Oy. Từ đó nêu các mối quan hệ giữa \(\sin \alpha \) và \(\sin \left( {{{180}^o} - \alpha } \right)\), giữa \(\cos \alpha \) và \(\cos \left( {{{180}^o} - \alpha } \right)\).
Tham khảo:
M, M’ là hai điểm trên nửa đường tròn đơn vị tương ứng với hai góc \(\alpha \) và \({180^o} - \alpha \).
Giả sử \(M\left( {{x_0};{y_o}} \right)\). Khi đó \(\cos \alpha = {x_0};\;\;\sin \alpha = {y_o}\)
Trường hợp 1: \(\alpha = {90^o}\)
Khi đó \(\alpha = {180^o} - \alpha = {90^o}\)
Tức là M và M’ lần lượt trùng nhau và trùng với B.
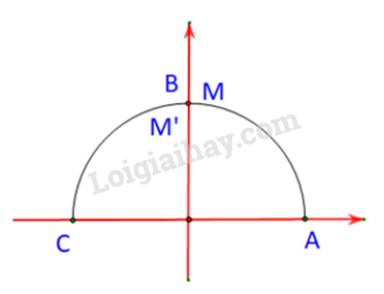
Và \(\left\{ \begin{array}{l}\cos \alpha = - \cos \left( {{{180}^o} - \alpha } \right) = 0;\\\sin \alpha = \sin \left( {{{180}^o} - \alpha } \right) = \sin {90^o} = 1.\\\cot \alpha = 0\end{array} \right.\)
Không tồn tại \(\tan \alpha \) với \(\alpha = {90^o}\)
Trường hợp 2: \(\alpha < {90^o} \Rightarrow {180^o} - \alpha > {90^o}\)
M nằm bên phải trục tung
M’ nằm bên trái trục tung
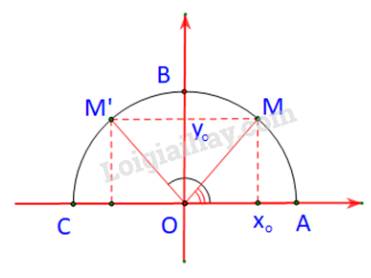
Dễ thấy: \(\widehat {M'OC} = {180^o} - \widehat {xOM'} = {180^o} - \left( {{{180}^o} - \alpha } \right) = \alpha = \widehat {xOM}\)
\( \Rightarrow \widehat {M'OB} = {90^o} - \widehat {M'OC} = {90^o} - \widehat {MOA} = \widehat {MOB}\)
Xét tam giác \(M'OB\) và tam giác \(MOB\) ta có:
\(OM = OM'\)
\(\widehat {M'OB} = \widehat {MOB}\)
OB chung
\(\begin{array}{l} \Rightarrow \Delta MOB = \Delta M'OB\\ \Rightarrow \left\{ \begin{array}{l}OM = OM'\\BM = BM'\end{array} \right.\end{array}\)
Hay OB là trung trực của đoạn thẳng MM’.
Nói cách khác M và M’ đối xứng với nhau qua trục tung.
Mà \(M\left( {{x_0};{y_o}} \right)\) nên \(M'\left( { - {x_0};{y_o}} \right)\)
\(\begin{array}{l}\cos \left( {{{180}^o} - \alpha } \right) = - {x_0} = - \cos \alpha ;\\\sin \left( {{{180}^o} - \alpha } \right) = {y_o} = \sin \alpha .\\ \Rightarrow \left\{ \begin{array}{l}\tan \left( {{{180}^o} - \alpha } \right) = - \tan \alpha \\\cot \left( {{{180}^o} - \alpha } \right) = - \cot \alpha \end{array} \right.\end{array}\)
Trường hợp 3: \(\alpha > {90^o} \Rightarrow {180^o} - \alpha < {90^o}\)
Khi đó M nằm bên trái trục tung và M’ nằm bên phải trục tung.
Tương tự ta cũng chứng minh được M và M’ đối xứng với nhau qua trục tung.
Như vậy
\(\begin{array}{l}\cos \left( {{{180}^o} - \alpha } \right) = - {x_0} = - \cos \alpha ;\\\sin \left( {{{180}^o} - \alpha } \right) = {y_o} = \sin \alpha .\\ \Rightarrow \left\{ \begin{array}{l}\tan \left( {{{180}^o} - \alpha } \right) = - \tan \alpha \\\cot \left( {{{180}^o} - \alpha } \right) = - \cot \alpha \end{array} \right.\end{array}\)
Kết luận: Với mọi \({0^o} < \alpha < {180^o}\), ta luôn có
\(\begin{array}{l}\cos \left( {{{180}^o} - \alpha } \right) = - \cos \alpha ;\\\sin \left( {{{180}^o} - \alpha } \right) = \sin \alpha .\\\tan \left( {{{180}^o} - \alpha } \right) = - \tan \alpha \;\;\;(\alpha \ne {90^o})\\\cot \left( {{{180}^o} - \alpha } \right) = - \cot \alpha \end{array}\)
Đúng 0
Bình luận (0)
a) Nêu nhận xét về vị trí điểm M trên nửa đường tròn đơn vị trong mỗi trường hợp sau:
\(\begin{array}{l}\alpha = {90^o};\\\alpha < {90^o};\\\alpha > {90^o}.\end{array}\)
b) Khi \({0^o} < \alpha < {90^o}\), nêu mối quan hệ giữa \(\cos \alpha ,\;\sin \alpha \) với hoành độ và tung độ của điểm M.
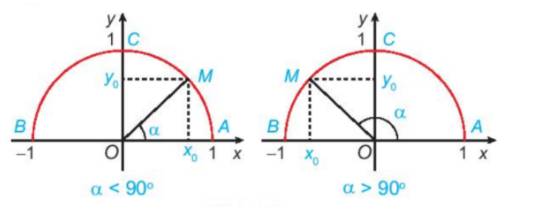
a) Khi \(\alpha = {90^o}\), điểm M trùng với điểm C. (Vì \(\widehat {xOC} = \widehat {AOC} = {90^o}\))
Khi \(\alpha < {90^o}\), điểm M thuộc vào cung AC (bên phải trục tung)
Khi \(\alpha > {90^o}\), điểm M thuộc vào cung BC (bên trái trục tung)
b) Khi \({0^o} < \alpha < {90^o}\) , ta có:
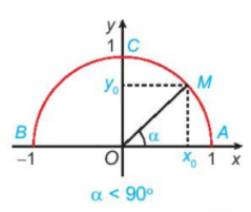
\(\begin{array}{l}\cos \alpha = \frac{{\left| {{x_0}} \right|}}{{OM}} = \left| {{x_0}} \right| = {x_0};\\\sin \alpha = \frac{{\left| {{y_0}} \right|}}{{OM}} = \left| {{y_o}} \right| = {y_o}\end{array}\)
Vì \(OM = R = 1\); \({x_0} \in \)tia \(Ox\)nên \({x_0} > 0\); \({y_0} \in \)tia \(Oy\)nên \({y_0} > 0\)
Vậy \(\cos \alpha \) là hoành độ \({x_0}\)của điểm M, \(\sin \alpha \) là tung độ \({y_0}\) của điểm M.
Đúng 0
Bình luận (0)
Trong hiện tượng khúc xạ ánh sáng xảy ra ở mặt phân cách giữa hai môi trường trong suốt nhất định, sin góc tới (sini) và sin góc khúc xạ (sin r ) luôn thỏa mãn hệ thức A. sin sin i r = hằng số. B. sin sin i r − = hằng số. C. sin i sin r = hằng số. D. sin sin i r + = hằng số.



