Tập hợp các số thực m để hàm số y = x 3 - 3 m x 2 + ( m + 2 ) x - m đạt cực tiểu tại x=1 là
A. 1
B. - 1
C. ○
D. ℝ
Cho hàm số y = 2 x 3 + 3 ( m − 1 ) x 2 + 6 ( m − 2 ) x − 1 . Gọi S là tập hợp tất cả các giá trị thực của m để hàm số có hai điểm cực trị đều thuộc (-2;1). Khi đó tập S là
A. S = (1;4)
B. S = ℝ \ 3
C. S = − ∞ ; 1 ∪ 4 ; + ∞
D. S = ( 1 ; 4 ) \ 3
Cho hàm số y = 2 x 3 - 3 m x 2 + 3 ( 5 m 2 + 1 ) x - 3 s i n x với m là tham số thực. Tìm tập hợp tất cả các giá trị của m để hàm số đồng biến trên (l;3).
A . m ≥ 1
B . m ≤ - 1
C . m > 0
D . m ∈ R
Tập hợp tất cả các giá trị thực của tham số m để hàm số \(y=\left|x^3-3x^2+m-4\right|\) có đúng 5 điểm cực trị là?
Tập hợp các số thực m để hàm số y = x 3 + ( m + 4 ) x 2 + ( 5 m + 2 ) x + m + 6 đạt cực tiểu tại
x = -2 là
A. O .
B. ℝ .
C. 2 .
D. - 2 .
Đáp án A
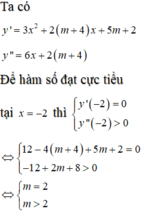
Vậy không có giá trị m thỏa mãn yêu cầu bài toán.
Cho hàm số đa thức bậc ba y=f(x) có đồ thị của các hàm số y=f(x), y=f '(x)như hình vẽ bên.Gọi S là tập hợp tất cả các giá trị nguyên của m để phương trình f(f(x)-m)+2f(x)=3(x+m) có đúng 3 nghiệm thực .Tổng các phần tử của S bằng
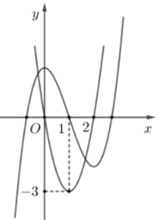
A. 0
B. -6
C. -7
D. -5
Ta có ![]()
![]()
Quan sát đồ thị có 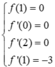
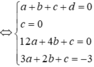

![]()
Đặt ![]() phương trình trở thành:
phương trình trở thành:
![]()
![]()
![]()
Khi đó ![]()
Phương trình này có 3 nghiệm phân biệt
![]()
Tổng các phần tử củaS bằng 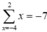
Chọn đáp án C.
Tìm tập hợp các giá trị của m để hàm số y=√ ( m - 2)x^2 - 2( m- 3)x + m - 1 có tập xác định là R
Hàm số xác định \(\Leftrightarrow\left(m-2\right)x^2-2\left(m-3\right)x+m-1\ge0\)
Đặt \(f\left(x\right)=\left(m-2\right)x^2-2\left(m-3\right)x+m-1\ge0\)
\(f\left(x\right)\ge0,\forall x\in R\Leftrightarrow\left\{{}\begin{matrix}a>0\\\Delta\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m-2>0\\\left[-2\left(m-3\right)\right]^2-4\left(m-2\right)\left(m-1\right)\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>2\\4\left(m^2-6m+9\right)-4\left(m^2-3m+2\right)\le0\end{matrix}\right.\)
\(\Leftrightarrow4m^2-24m+36-4m^2+12m-8\le0\)
\(\Leftrightarrow-12m+28\le0\)
\(\Leftrightarrow m\le\dfrac{7}{3}\)
\(KL:m\in(2;\dfrac{7}{3}]\)
Cho hàm số y = 1 3 x 3 + 2 x 2 + ( m + 2 ) x - m . Tìm tập hợp S tất cả các giá trị thực của tham số m để hàm số đồng biến trên ℝ
A. S = ( - ∞ ; 2 ]
B. S = ( - ∞ ; 2 )
C. S = [ 2 ; + ∞ )
D. S = ( 2 ; + ∞ )
Tìm tập hợp tất cả các giá trị thực của tham số m để hàm số y = | x | 3 - ( 2 m + 1 ) x 2 + 3 m | x | - 5 có 3 điểm cực trị.
A. - ∞ ; 1 4
B. 1 ; + ∞
C. ( - ∞ ; 0 ]
D. 0 ; 1 4 ∪ 1 ; + ∞
Tìm tập hợp tất cả các giá trị thực của tham số m để hàm số y = 1 3 x 3 - ( m + 1 ) x 2 + ( m 2 + 2 m ) x - 3 nghịch biến trên khoảng ( 0 ; 1 )
A. [ - 1 ; + ∞ )
B. ( - ∞ ; 0 ]
C. [ - 1 ; 0 ]
D. [ 0 ; 1 ]