Hàm số f(x) = 2.sinx + sin2x trên đoạn 0 , 3 π 2 có giá trị lớn nhất là M, giá trị nhỏ nhất là m. Khi đó M+m bằng:
A . - 3 3
B . 3 3
C . - 3 3 4
D . 3 3 2
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:
a) f(x) = ( 25 - x 2 ) trên đoạn [-4; 4]
b) f(x) = | x 2 – 3x + 2| trên đoạn [-10; 10]
c) f(x) = 1/sinx trên đoạn [π/3; 5π/6]
d) f(x) = 2sinx + sin2x trên đoạn [0; 3π/2]
a) 
f′(x) > 0 trên khoảng (-4; 0) và f’(x) < 0 trên khoảng (0; 4).
Hàm số đạt cực đại tại x = 0 và f C Đ = 5
Mặt khác, ta có f(-4) = f(4) = 3
Vậy 
d) f(x) = | x 2 − 3x + 2| trên đoạn [-10; 10]
Khảo sát sự biến thiên và vẽ đồ thị của hàm số g(x) = x 2 – 3x + 2.
Ta có:
g′(x) = 2x − 3; g′(x) = 0 ⇔ x = 3/2
Bảng biến thiên:

Vì

nên ta có đồ thị f(x) như sau:

Từ đồ thị suy ra: min f(x) = f(1) = f(2) = 0; max = f(x) = f(−10) = 132
e) 
f′(x) < 0 nên và f’(x) > 0 trên (π/2; 5π/6] nên hàm số đạt cực tiểu tại x = π/2 và f C T = f(π/2) = 1
Mặt khác, f(π/3) = 2√3, f(5π/6) = 2
Vậy min f(x) = 1; max f(x) = 2
g) f(x) = 2sinx + sin2x trên đoạn [0; 3π/2]
f′(x) = 2cosx + 2cos2x = 4cos(x/2).cos3(x/2)
f′(x) = 0
⇔ 
Ta có: f(0) = 0,

Từ đó ta có: min f(x) = −2 ; max f(x) = 3√3/2
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau: f(x) = 2sinx + sin2x trên đoạn [0; 3 π /2]
f(x) = 2sinx + sin2x trên đoạn [0; 3 π /2]
f′(x) = 2cosx + 2cos2x = 4cos(x/2).cos3(x/2)
f′(x) = 0
⇔ 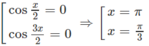
Ta có: f(0) = 0,
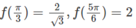
Từ đó ta có: min f(x) = −2 ; max f(x) = 3 3 /2
Cho hàm số y=f(x) liên tục trên đoạn [0;π/3].Biết f’(x).cosx+f(x).sinx=1, x ϵ [0;π/3] và f(0)=1. Tính tích phân I = ∫ 0 π 3 f x d x
A. 1/2 + π/3
B. 3 + 1 2
C. 3 - 1 2
D. 1/2
\(f\left(x\right)=e^{sinx}-sinx-1\)
\(\Rightarrow f'\left(x\right)=cosx.e^{sinx}-cosx=cosx\left(e^{sinx}-1\right)\)
\(f'\left(x\right)=0\Leftrightarrow\left[{}\begin{matrix}cosx=0\\sinx=0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{\pi}{2}\\x=\pi\end{matrix}\right.\)
\(f\left(0\right)=0\) ; \(f\left(\dfrac{\pi}{2}\right)=e-2\) ; \(f\left(\pi\right)=0\)
\(\Rightarrow f\left(x\right)_{min}=0\) ; \(f\left(x\right)_{max}=e-2\)
Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số f(x) = sinx (1+cosx) trên đoạn 0 ; π
A. M = 3 3 2 ; m = 1
B. M = 3 3 4 ; m = 0
C. M = 3 3 ; m = 1
D. M = 3 ; m = 1
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau: f(x) = 1/sinx trên đoạn [ π /3; 5 π /6]
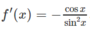
f′(x) < 0 nên và f’(x) > 0 trên ( π /2; 5 π /6] nên hàm số đạt cực tiểu tại x = π /2 và f CT = f( π /2) = 1
Mặt khác, f( π /3) = 2 3 , f(5 π /6) = 2
Vậy min f(x) = 1; max f(x) = 2
Hàm số y = sinx đồng biến trên đoạn nào dưới đây ?
A . [ π ; 2π ]
B . [-π ; π ]
C . [ 0 ; π ]
D . [ 0 ; \(\dfrac{\pi}{2}\)]
????????????????????
Tìm giá trị lớn nhất của hàm số y = x + sin 2 x trên đoạn [ 0 ; π ]
A. π
B. 0
C. 3 π 4 + 1 2
D. 3 π 4
Đáp án là A.
Ta có: y , = 1 + 2 sin x cos x = 1 + sin 2 x
y , = 0 ⇔ x = - π 4 + k π , k ∈ ℤ
Vì x ∈ 0 ; π nên x = 3 π 4
Tính được: y ( 0 ) = 0 ; y ( π ) = π ; y ( 3 π 4 ) = 3 π 4 + 1 2
Vậy: m a x [ 0 ; π ] y = y ( π ) = π .
Cho hàm số f thỏa mãn f cot x = sin 2 x + cos 2 x , ∀ x ∈ 0 ; π . Giá trị lớn nhất của hàm số g x = f sin 2 x . f cos 2 x trên ℝ là
A. 6 125 .
B. 1 20 .
C. 19 500 .
D. 1 25 .
Đáp án là D

h 1 2 = 1 25 k h i x = π 4 + k π 2