Cho hàm số y = 4 x 3 - 6 x 2 + 1 có đồ thị là đường cong trong hình dưới đây.
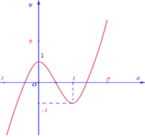
Khi đó phương trình 4 4 x 3 - 6 x 2 + 1 3 - 6 4 x 3 - 6 x 2 + 1 + 1 = 0 có bao nhiêu nghiệm thực.
A. 9
B. 6
C. 7
D. 3
1.Cho hàm số y = g(x) = x - 4. Khi đó g(-2) bằng
A.-2 B.2 C.-6 D.6
2.Cho hàm số y = f(x) = -3x+ 5. Nếu f(x) = -7 thì x bằng
A.2/3 B.-4 C.2 D.4
Bài 1: Tìm m để các hàm số sau là hàm số bậc nhất
a) y= ( m - 2 )x - \(\dfrac{2}{3}\) b) y= ( 4 - 2022m )x - 2 c) y= \(\sqrt{1-2m}\)x + m - 3
Bài 2: Cho đồ thị hàm số y= -2x + 3
a) Xác định hệ số a,b
b) Các điểm A( -2 ; 7) ; B(\(\sqrt{2}\) ; 6)
c) Tìm tọa độ điểm M thuộc ( d ) có tung độ = 11
d) Tìm tọa độ điểm C thuộc ( d ), biết rằng hoành độ của điểm C gấp 3 tung độ của nó
e) Tìm tọa độ điểm E thuộc ( d ), biết rằng tung độ của điểm E và hoành độ là 2 số đối nhau
a) cho hàm số y=(f)x=x^6+1/x^3.cmr f(1/2)=f(x)
b) cho hàm số y=(f)x=x^2+1/x^2.CMR f(x)=f(-x)
c) cho hàm số y=(f)x=5^x. Tính f(x+1)-f(x)
HELPPPPPPPPPPPPP ME!
Câu 25. Cho hàm số \(y = \dfrac{x + 1}{x - 1}, y = -x^3+x^2-3x+1, y = x^4 + 2x^2 +2.\) Trong các hàm số trên, có bao nhiêu hàm số đơn điệu trên \(R\)?
A. 1. B. 3. C. 0. D. 2.
\(y'_1=-\dfrac{2}{\left(x-1\right)^2}\) nghịch biến trên R/{1}
\(y'_2=-3x^2+2x-3\) có nghiệm khi y' = 0
\(y'_3=4x^3+4x\) có nghiệm khi y' = 0
Vậy không có hàm số đơn điệu trên R.
Hàm số y được cho bảng sau:
| x | 0 | 1 | 2 | 3 | 4 |
| y | 0 | 2 | 4 | 6 | 8 |
Viết tất cả các cặp giá trị tương ứng (x; y) của hàm số trên
Tất cả các cặp giá trị tương ứng (x; y) là
(0; 0) ; (1; 2) ; (2; 4) ; (3; 6) ; (4; 8)
Cho hàm số y=f(x)=\(\sqrt{x}\) Trong các điểm sau,điểm nào thuộc đồ thị của hàm số?
A(4;2) B(2;1) C(8;2\(\sqrt{2}\)) D(4-2\(\sqrt{3}\); 1-\(\sqrt{3}\)) E(6+2\(\sqrt{5}\);1+\(\sqrt{5}\))
Thay x=4 vào \(y=f\left(x\right)=\sqrt{x}\), ta được
\(f\left(4\right)=\sqrt{4}=2\)
=>A(4;2) thuộc đồ thị hàm số \(y=f\left(x\right)=\sqrt{x}\)
Thay \(x=2\) vào \(y=f\left(x\right)=\sqrt{x}\), ta được;
\(f\left(2\right)=\sqrt{2}>1\)
=>B(2;1) không thuộc đồ thị hàm số \(y=f\left(x\right)=\sqrt{x}\)
Thay \(x=8\) vào \(y=\sqrt{x}\), ta được:
\(y=\sqrt{8}=2\sqrt{2}\)
=>\(C\left(8;2\sqrt{2}\right)\) thuộc đồ thị hàm số \(y=\sqrt{x}\)
Thay \(x=4-2\sqrt{3}\) vào \(y=\sqrt{x}\), ta được:
\(y=\sqrt{4-2\sqrt{3}}=\sqrt{3-2\cdot\sqrt{3}\cdot1+1}\)
\(=\sqrt{\left(\sqrt{3}-1\right)^2}=\left|\sqrt{3}-1\right|=\sqrt{3}-1< >1-\sqrt{3}\)
=>\(D\left(4-2\sqrt{3};1-\sqrt{3}\right)\) không thuộc đồ thị hàm số \(y=f\left(x\right)=\sqrt{x}\)
Thay \(x=6+2\sqrt{5}\) vào \(y=f\left(x\right)=\sqrt{x}\), ta được:
\(f\left(6+2\sqrt{5}\right)=\sqrt{6+2\sqrt{5}}=\sqrt{\left(\sqrt{5}+1\right)^2}\)
\(=\left|\sqrt{5}+1\right|=\sqrt{5}+1\)
vậy: \(E\left(6+2\sqrt{5};1+\sqrt{5}\right)\) thuộc đồ thị hàm số \(y=f\left(x\right)=\sqrt{x}\)
Cho hàm số y = f(x) = 1/2x + 5
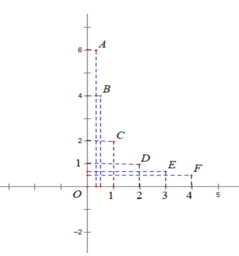
a) Biểu diễn các điểm sau trên mặt phẳng tọa độ Oxy:
A(1/3; 6), B(1/2; 4), C(1; 2), D(2; 1), E(3; 2/3), F(4; 1/2).
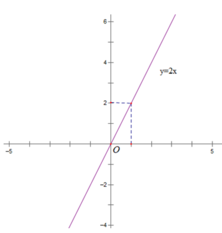
b) Vẽ đồ thị của hàm số y = 2x.
a)
b)Bảng giá trị
| x | 0 | 1 |
| y = 2x | 0 | 2 |
Đồ thị hàm số y = 2x đi qua 2 điểm (0; 0) và (1; 2)
Cho hàm số y = 3|x − 2| − |2x − 6| có đồ thị (C). Tìm giá trị lớn nhất và nhỏ nhất của hàm số trên với x ∈ [−3; 4]
A. max − 3 ; 4 y = 4
B. min y = − 2 − 3 ; 4
C. Cả A, B đều đúng
D. Cả A, B đều sai
Câu4 :Cho hàm số y = f(x) = 2x. Khẳng định nào sau đây đúng? A. f(0) = 0 B. f(1) = 6 C. f(-1) = 10 D. f(2) = -4 Câu 5:Một hàm số được cho bẳng công thức y = f(x) = x2 ( x bình phương) Khẳng định nào sau đây đúng? A. f(1) = 6 Câu6:Cho hàm số y = f(x) = 2 + 8x. Khẳng định nào sau đây đúng? A. f(0) = 0 B. f(1) = 10 C. f(-1) = 10 D. f(2) = -4 Câu7:Một hàm số được cho bẳng công thức y = f(x) = 2x. Tính f(-5) + f(5). KẾT QUẢ ĐÚNG LÀ A. 0 B. 25 C. 50 D. 10
tính đạo hàm của các hàm số sau
a) \(y=x^2+3x-6x^6+\dfrac{2x-3}{x-1}\)
b) \(y=3x^2-4x+\sqrt{2x^2-3x+1}\)
c) \(y=\sqrt{4x^2-3x+1}-4\)
a: \(y'=\left(x^2\right)'+\left(3x\right)'-\left(6x^6\right)'+\left(\dfrac{2x-3}{x-1}\right)'\)
\(=2x+3-6\cdot6x^5+\dfrac{\left(2x-3\right)'\left(x-1\right)-\left(2x-3\right)\left(x-1\right)'}{\left(x-1\right)^2}\)
\(=-36x^5+2x+3+\dfrac{2\left(x-1\right)-2x+3}{\left(x-1\right)^2}\)
\(=-36x^5+2x+3+\dfrac{1}{\left(x-1\right)^2}\)
b: \(\left(\sqrt{2x^2-3x+1}\right)'=\dfrac{\left(2x^2-3x+1\right)'}{2\sqrt{2x^2-3x+1}}\)
\(=\dfrac{4x-3}{2\sqrt{2x^2-3x+1}}\)
\(y'=3\cdot2x-4+\dfrac{4x-3}{2\sqrt{2x^2-3x+1}}\)
\(=6x-4+\dfrac{4x-3}{2\sqrt{2x^2-3x+1}}\)
c: \(\left(\sqrt{4x^2-3x+1}\right)'=\dfrac{\left(4x^2-3x+1\right)'}{2\sqrt{4x^2-3x+1}}\)
\(=\dfrac{8x-3}{2\sqrt{4x^2-3x+1}}\)
\(y'=\left(\sqrt{4x^2-3x+1}\right)'-4'=\dfrac{8x-3}{2\sqrt{4x^2-3x+1}}\)