Hình trụ (T) được sinh ra khi quay hình chữ nhật ABCD quanh cạnh AB. Biết AC=2a 2 và A C B ⏜ = 45 0 . Diện tích toàn phần S t p của hình trụ (T) là:
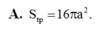
![]()
![]()
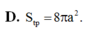
Hình trụ (T) được sinh ra khi quay hình chữ nhật ABCD xung quanh cạnh AB. Biết A C = 2 a 2 và A C B ^ = 45 ° . Diện tích toàn phần của hình trụ (T) bằng
A. 10 πa 2
B. 16 πa 2
C. 12 πa 2
D. 8 πa 2
Hình trụ (T) được sinh ra khi quay hình chữ nhật ABCD quanh cạnh AB. Biết A C = 2 a 2 và A C B ^ = 45 0 . Diện tích toàn phần S t p của hình trụ (T) là
A. S t p = 16 π a 2 .
B. S t p = 10 π a 2 .
C. S t p = 12 π a 2 .
D. S t p = 8 π a 2 .
Cho hình trụ (T) được sinh ra khi quay hình chữ nhật ABCD quanh cạnh AB. Biết A C = 2 3 a và góc A C B ^ = 45 0 . Diện tích toàn phần S t p của hình trụ (T) là:
A. 12 π a 2 .
B. 8 π a 2 .
C. 24 π a 2 .
Đáp án C
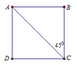
Vì ABCD là hình chữ nhật và A C B ⏜ = 45 ° nên ABCD là hình vuông.
Ta có: 2. A B 2 = 2 3 a 2 ⇔ A B = 6 a
S t p = 2 π B C 2 + 2 π . B C = 2 π . B C . A B = 2 π . 6 a 2 + 2 π . 6 a 2 = 24 π a 2
Cho hình chữ nhật ABCD có AB=a, AC=2a. Tính diện tích xung quanh của hình trụ nhận được khi quay hình chữ nhật quanh cạnh AB
A. a 2 2 3 3
B. 3 a 2
C. 2 3 a 2
D. 2 3 π a 2
Trong không gian, cho hình chữ nhật ABCD có AD=a, AC=2a. Độ dài đường sinh của hình trụ nhận được khi quay hình chữ nhật ABCD xung quanh trục AB là
![]()
![]()
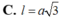
![]()
Cho hình chữ nhật ABCD có chiều dài A B = 2 A D . Quay hình chữ nhật quay quanh cạnh AB sinh ra khối trụ có thể tích V 1 và quay hình chữ nhật đó quanh cạnh AD sinh ra hình
trụ có thể tích V 2 . Tỉ số V 1 V 2 là
A. 27 π 2 .
B. 1 2 .
C. π 2 .
D. 27
Cho hình trụ có được khi quay hình chữ nhật ABCD quanh trục AB. Biết rằng AB = 2AD = 2a. Thể tích khối trụ đã cho theo a là:
A. 2π a 3
B. π a 3
C. 2π a 3 /3
D. π a 3 /2
Đáp án A
Từ giả thiết ta có h = AB = 2a, r = AD = a. Khi đó ta có thể tích khối trụ là: V = π r 2 h = 2π a 3 .
Trong không gian cho hình chữ nhật ABCD có AD = a , AC = 3 a . . Tính theo a độ dài đường sinh l của hình trụ, nhận được khi quay hình chữ nhật ABCD xung quanh trục AB.
A. 10 a
B. 2 2 a
C. 3 a
D. 2 3 a
Cho hình chữ nhật ABCD có tỉ lệ hai cạnh A B : A D = 2 : 3 . Khi quay hình chữ nhật xung quanh cạnh AB ta thu được hình trụ có thể tích V 1 , khi quay hình chữ nhật quanh cạnh AD ta thu được hình trụ có thể tích V 2 . Tính tỉ số thể tích V 1 V 2 .
A. 3 2 .
B. 2 3 .
C. 2 5 .
D. 3 5 .
Đáp án A
Khi quay hình chữ nhật xung quanh cạnh AB thì bán kính hình trụ lúc này R 1 = A D , chiều cao bằng h 1 = A B . Khi đó V 1 = π R 1 2 h 1 = π . A D 2 . A B .
Khi quay hình chữ nhật xung quanh cạnh AD thì bán kính hình trụ lúc này là R 2 = A B , chiều cao h 2 = A D . Khi đó V 2 = π R 2 2 h 2 = π A B 2 . A D .
Do đó, tỉ số thể tích là V 1 V 2 = π . A D 2 . A B π . A B 2 . A D = A D A B = 3 2 .