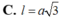Các câu hỏi tương tự
Trong không gian cho hình chữ nhật ABCD có
A
B
a
,
A
C
a
5
. Tính diện tích xung quanh
S
x
q
của hình trụ khi quay đường gấp khúc BCDA quanh trục AB A.
S
x
q
2
π
a
2
.
B. ...
Đọc tiếp
Trong không gian cho hình chữ nhật ABCD có A B = a , A C = a 5 . Tính diện tích xung quanh S x q của hình trụ khi quay đường gấp khúc BCDA quanh trục AB
A. S x q = 2 π a 2 .
B. S x q = 4 π a 2 .
C. S x q = 2 a 2 .
D. S x q = 4 a 2 .
Trong không gian cho hình chữ nhật ABCD có
A
B
a
,
A
C
a
5
. Tính diện tích xung quanh
S
x
q
của hình trụ khi quay đường gấp khúc BCDA quanh trục AB A.
S
x
q
2
π
a
2
.
B.
S
x...
Đọc tiếp
Trong không gian cho hình chữ nhật ABCD có A B = a , A C = a 5 . Tính diện tích xung quanh S x q của hình trụ khi quay đường gấp khúc BCDA quanh trục AB
A. S x q = 2 π a 2 .
B. S x q = 4 π a 2 .
C. S x q = 2 a 2 .
D. S x q = 4 a 2 .
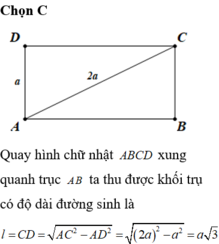
Cho hình chữ nhật ABCD có AC 2AD 2a. Quay quanh trục AB đường gấp khúc ADCB ta được hình trụ có diện tích xung quanh là: A. 6π
a
2
B. 3π
a
2
C. 2π
a
2
3
D. π
a
2
6
Đọc tiếp
Cho hình chữ nhật ABCD có AC = 2AD = 2a. Quay quanh trục AB đường gấp khúc ADCB ta được hình trụ có diện tích xung quanh là:
A. 6π a 2
B. 3π a 2
C. 2π a 2 3
D. π a 2 6
Trong không gian cho hình chữ nhật ABCD có AB1, AD2. Gọi M, N lần lượt là trung điểm AD và BC. Quay hình chữ nhật đó xung quanh trục MN ta được một hình trụ. Tính diện tích toàn phần của hình trụ đó?
Đọc tiếp
Trong không gian cho hình chữ nhật ABCD có AB=1, AD=2. Gọi M, N lần lượt là trung điểm AD và BC. Quay hình chữ nhật đó xung quanh trục MN ta được một hình trụ. Tính diện tích toàn phần của hình trụ đó?
![]()
![]()
![]()
![]()
Trong không gian, cho hình chữ nhật ABCD có
A
B
1
v
à
A
D
2
.
Gọi M, N lần lượt là trung điểm của AD và BC. Quay hình chữ nhật đó xung quanh trục MN, ta được một hình trụ. Tính diện tích toàn phần
S
t
p
của hình trụ đó. A.
S
t...
Đọc tiếp
Trong không gian, cho hình chữ nhật ABCD có A B = 1 v à A D = 2 . Gọi M, N lần lượt là trung điểm của AD và BC. Quay hình chữ nhật đó xung quanh trục MN, ta được một hình trụ. Tính diện tích toàn phần S t p của hình trụ đó.
A. S t p = 6 π
B. S t p = 2 π
C. S t p = 4 π
D. S t p = 10 π
Trong không gian, cho hình chữ nhật ABCD có AB1 và AD2. Gọi M,N lần lượt là trung điểm của AD và BC. Quay hình chữ nhật đó xung quanh trục MN , ta được một hình trụ. Tính diện tích toàn phần Stp của hình trụ đó.
Đọc tiếp
Trong không gian, cho hình chữ nhật ABCD có AB=1 và AD=2. Gọi M,N lần lượt là trung điểm của AD và BC. Quay hình chữ nhật đó xung quanh trục MN , ta được một hình trụ. Tính diện tích toàn phần Stp của hình trụ đó.
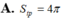
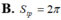
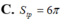
![]()
Trong không gian, cho hình chữ nhật ABCD có AB1 và AD2. Gọi M, N lần lượt là trung điểm của AB và CD. Quay hình chữ nhật đó xung quanh trục MN, ta được một hình trụ. Tính thể tích V của khối trụ tạo bởi hình trụ đó. A.
π
2
B.
π
C.
2
π
D. 4
π
Đọc tiếp
Trong không gian, cho hình chữ nhật ABCD có AB=1 và AD=2. Gọi M, N lần lượt là trung điểm của AB và CD. Quay hình chữ nhật đó xung quanh trục MN, ta được một hình trụ. Tính thể tích V của khối trụ tạo bởi hình trụ đó.
A. π 2
B. π
C. 2 π
D. 4 π
Trong không gian cho ABCD là hình chữ nhật,
A
B
2
,
A
D
1
. Đường thẳng d nằm trong mặt phẳng (ABCD) không có điểm chung với hình chữ nhật ABCD, song song với cạnh AB và cách AB một khoảng bằng a. Gọi V là thể tích của khối tròn xoay T, nhận được khi quay hình chữ nhật ABCD xung quanh trục d. Cho biết
d
A
B
,
d...
Đọc tiếp
Trong không gian cho ABCD là hình chữ nhật, A B = 2 , A D = 1 . Đường thẳng d nằm trong mặt phẳng (ABCD) không có điểm chung với hình chữ nhật ABCD, song song với cạnh AB và cách AB một khoảng bằng a. Gọi V là thể tích của khối tròn xoay T, nhận được khi quay hình chữ nhật ABCD xung quanh trục d. Cho biết d A B , d < d C D , d . Tính a biết rằng thể tích khối T gấp 3 lần thể tích của khối cầu có đường kính AB.
![]()
![]()
![]()
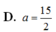
Trong không gian cho hình chữ nhật ABCD có AB4, BC2. Gọi P, Q lần lượt là các điểm trên cạnh AB và CD sao cho BP1, QD3QC. Quay hình chữ nhật APQD xung quanh trục PQ ta được một hình trụ. Diện tích xung quanh của hình trụ đó bằng
Đọc tiếp
Trong không gian cho hình chữ nhật ABCD có AB=4, BC=2. Gọi P, Q lần lượt là các điểm trên cạnh AB và CD sao cho BP=1, QD=3QC. Quay hình chữ nhật APQD xung quanh trục PQ ta được một hình trụ. Diện tích xung quanh của hình trụ đó bằng
![]()
![]()
![]()
![]()