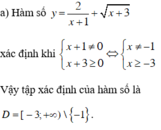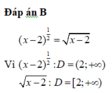Tìm tập xác định của các hàm số sau: y = x 3 - 3 x 2 + 2 x 1 4
PB
Những câu hỏi liên quan
I. HÀM SỐ, TXĐ, CHẴN LẺ, ĐƠN ĐIỆU, ĐỒ THỊ.1. TXĐ CỦA HÀM SỐCâu 1.Tìm tập xác định của hàm số ydfrac{sqrt{x-1}}{x-3}Câu 2.Tìm tập xác định của hàm số y sqrt[3]{x-1}Câu 3. Tìm tập xác định của hàm số ydfrac{sqrt[3]{1-x}+3}{sqrt{x+3}}Câu 4. Tìm tập xác định của hàm số ysqrt{left|x-2right|}
Đọc tiếp
I. HÀM SỐ, TXĐ, CHẴN LẺ, ĐƠN ĐIỆU, ĐỒ THỊ.
1. TXĐ CỦA HÀM SỐ
Câu 1.Tìm tập xác định của hàm số y=\(\dfrac{\sqrt{x-1}}{x-3}\)
Câu 2.Tìm tập xác định của hàm số y= \(\sqrt[3]{x-1}\)
Câu 3. Tìm tập xác định của hàm số y=\(\dfrac{\sqrt[3]{1-x}+3}{\sqrt{x+3}}\)
Câu 4. Tìm tập xác định của hàm số y=\(\sqrt{\left|x-2\right|}\)
ĐKXĐ:
a. \(\left\{{}\begin{matrix}x-1\ge0\\x-3\ne0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x\ge1\\x\ne3\end{matrix}\right.\) \(\Rightarrow D=[1;+\infty)\backslash\left\{3\right\}\)
b. \(D=R\)
c. \(x+3>0\Rightarrow x>-3\Rightarrow D=\left(-3;+\infty\right)\)
d. \(\left|x-2\right|\ge0\Rightarrow x\in R\Rightarrow D=R\)
Đúng 1
Bình luận (0)
Tìm tập xác định của các hàm số sau
- y= 3/ 1+ x^2
- y= 2/ |x|+1
Tìm tập xác định của các hàm số sau: y = x 2 - 4 x + 3 - 2
Hàm số xác định khi x 2 − 4x + 3 ≠ 0 hay x ≠ 1; x ≠ 3.
Vậy tập xác định của hàm số đã cho là R \ {1;3}.
Đúng 0
Bình luận (0)
Tìm tập xác định của các hàm số y = 2 x + 1 + x + 3
Tìm tập xác định của các hàm số sau: a) y2x^3+3x+1;b) ydfrac{x-1}{x^2-3x+2} ;��−1�2−3�+c) ysqrt{x+1}+sqrt{1-x}.
Đọc tiếp
Tìm tập xác định của các hàm số sau:
a) \(y=2x^3+3x+1\);
b) \(y=\dfrac{x-1}{x^2-3x+2}\) ;
c) \(y=\sqrt{x+1}+\sqrt{1-x}\).
a) Hàm \(y = 2{x^3} + 3x + 1\) là hàm đa thức nên có tập xác định \(D = \mathbb{R}\)
b) Biểu thức \(\frac{{x - 1}}{{{x^2} - 3x + 2}}\)có nghĩa khi \({x^2} - 3x + 2 \ne 0 \Leftrightarrow x \ne 1\)và \(x \ne 2\)
Vậy tập xác định của hàm số đã cho là \(D = \mathbb{R}/\left\{ {1;2} \right\}\)
c) Biểu thức \(\sqrt {x + 1} + \sqrt {1 - x} \) có nghĩa khi \(x + 1 \ge 0\) và \(1 - x \ge 0\), tức là \( - 1 \le x \le 1\)
Vậy tập xác định của hàm số đã cho là \(D = \left[ { - 1;1} \right]\)
Đúng 0
Bình luận (0)
Cho hàm số
y
(
x
-
2
)
-
1
2
Bạn Toán tìm tập xác định của hàm số bằng cách như sau:Bước 1: Ta có
y
1
(
x
-
2
)
1
2...
Đọc tiếp
Cho hàm số y = ( x - 2 ) - 1 2 Bạn Toán tìm tập xác định của hàm số bằng cách như sau:
Bước 1: Ta có y = 1 ( x - 2 ) 1 2 = 1 x - 2
Bước 2: Hàm số xác định ⇔ x - 2 > 0 ⇔ x > 2
Bước 3: Vậy tập xác định của hàm số là D = ( 2 ; + ∞ )
Lời giải trên của bạn toán đúng hay sai? Nếu sai thì sai ở bước nào?
A. Bước 3
B. Bước 1
C. Đúng
D. Bước 2
Tìm tập xác định của các hàm số
y
1
x
+
3
v
ớ
i
x
≥
1
2...
Đọc tiếp
Tìm tập xác định của các hàm số y = 1 x + 3 v ớ i x ≥ 1 2 - x v ớ i x < 1
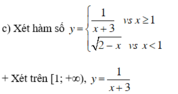
Hàm số xác định khi x + 3 ≠ 0 (luôn thỏa mãn với mọi x ≥ 1).
Vậy hàm số luôn xác định trên [1; +∞).
+ Xét trên (–∞; 1), .
Hàm số xác định khi 2 – x ≥ 0 ⇔ x ≤ 2 (Luôn thỏa mãn với mọi x < 1).
Vậy hàm số luôn xác định trên (–∞; 1).
Kết luận: Hàm số xác định trên R.
Đúng 0
Bình luận (0)
Tìm tập xác định của các hàm số sau: y = log 6 3 x + 2 1 - x
Xét bốn mệnh đề sau:
1
: Hàm số
y
s
inx
có tập xác định là
R
2
: Hàm số
y
c
osx
có tập xác định là
R
3
Hàm số
y
tan
x
có tập xác định là
R
4
Hàm số
y
cot...
Đọc tiếp
Xét bốn mệnh đề sau:
1 : Hàm số y = s inx có tập xác định là R
2 : Hàm số y = c osx có tập xác định là R
3 Hàm số y = tan x có tập xác định là R
4 Hàm số y = cot x có tập xác định là R
Tìm số phát biểu đúng.
A. 3
B. 2
C. 4
D. 1
Đáp án là B
• Hàm số y = sin x ; y = cos x có tập xác định D = ℝ .
• Hàm số y = tan x & y = cot x có tập xác định lần lượt D = ℝ \ π 2 + k π ; D = ℝ \ k π .
Đúng 0
Bình luận (0)
Tìm tập xác định của các hàm số sau: y = x 2 + x - 6 - 1 3
Hàm số xác định khi x 2 + x – 6 > 0 hay x < -3 và x > 2.
Vậy tập xác định là (− ∞ ; −3) ∪ (2; + ∞ ).
Đúng 0
Bình luận (0)