Tìm cực trị của các hàm số sau: y = x - 4 2 x 2 - 2 x + 5
PB
Những câu hỏi liên quan
Tìm các điểm cực trị của các hàm số sau: y = x + ln(x + 1)
Tìm cực trị của các hàm số sau: y = x + 2 2 . x - 3 3
TXĐ: R
y′ = 2(x + 2). x - 3 3 + 3 x + 2 2 . x - 3 2 = 5x(x + 2). x - 3 2
y′= 0 ⇔ 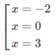
Bảng biến thiên:

Từ đó suy ra y CĐ = y(-2) = 0; y CT = y(0) = -108.
Đúng 0
Bình luận (0)
Tìm cực trị của các hàm số sau: y = (7 - x) x + 5 3
Hàm số xác định trên khoảng (− ∞ ;+ ∞ ).
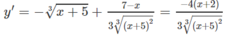
Bảng biến thiên:
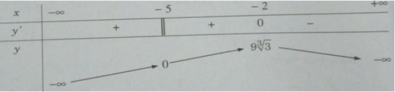
Vậy
y
CD
= y(−2) = 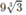
Đúng 0
Bình luận (0)
Tìm cực trị của các hàm số sau: y = x + 1 x 2 + 8
TXĐ : R
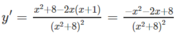
y′= 0 ⇔ 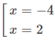
Bảng biến thiên:
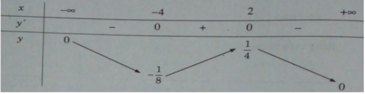
Hàm số đạt cực đại tại x = 2, cực tiểu tại x = -4 và y CD = y(2) = 1/4; y CT = y(−4) = −1/8
Đúng 0
Bình luận (0)
Tìm cực trị của các hàm số sau: y = x - 6 x 2 3
TXĐ: R
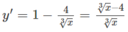
y′ = 0 ⇔ x = 64
Bảng biến thiên:
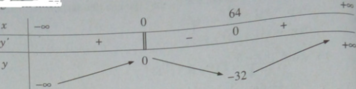
Vậy ta có y CD = y(0) = 0 và y CT = y(64) = -32.
Đúng 0
Bình luận (0)
Nêu cách tìm cực đại, cực tiểu của hàm số nhờ đạo hàm. Tìm các cực trị của hàm số \(y = x^4 – 2x^2 + 2\)
Xét hàm số : y = x4 – 2x2 + 2
Có đạo hàm là: y’ = 4x3 – 4x = 0 ⇔ x = 0, x = 1, x = -1
Đạo hàm cấp hai: y’’ = 12x2 – 4
y’’(0) = -4 < 0 ⇒ điểm cực đại xCD =0
y’’(-1) = 8 > 0, y’’(-1) = 8 > 0
⇒ các điểm cực tiểu xCT = -1, xCT = 1
Đúng 0
Bình luận (0)
Câu 3 Để đồ thị hàm số \(y=-x^4-\left(m-3\right)x^2+m+1\) có điểm cực đạt mà không có điểm cực tiểu thì tất cả giá trị thực của tham số m là
Câu 4 Cho hàm số \(y=x^4-2mx^2+m\) .Tìm tất cả các giá trị thực của m để hàm số có 3 cực trị
Tìm cực trị của các hàm số sau: y = x 2 + x - 5 x + 1
TXĐ: R\{-1}
![]()
Hàm số đồng biến trên các khoảng và do đó không có cực trị.
Đúng 0
Bình luận (0)
Tìm các điểm cực trị của hàm số y = x 3 5 ( 4 - x ) , x>0.
A. x=2
B. x = 3 2
C. x=6
D. x=4
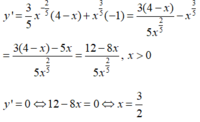
y’ đổi dấu khi đi qua điểm x = 3 2 nên hàm số có một điểm cực trị là x = 3 2
Chọn B
Đúng 0
Bình luận (0)


