Cho tam giác đều ABC, điểm M thuộc cạnh AB. So sánh độ dài các cạnh của tam giác BMC.
PB
Những câu hỏi liên quan
Cho tam giác ABC đều, điểm D thuộc cạnh AB. So sánh độ dài các cạnh của tam giác BDC.
cho tam giác đều abc, điểm d thuộc cạnh ab. So sánh độ dài các cạnh tam giác BCD
cho tam giác abc có góc a = 60 độ góc c < góc B < 90 độ
a, cm ab<ac
b cm trên cạnh ac lấy điểm m sao cho am = ab .Chứng minh tam giác abm là tam giác đều
c, so sánh các cạnh của tam giác abc
a: góc C<góc B
=>AB<AC
b: Xét ΔABM co AB=AM và góc A=60 độ
nên ΔAMB đều
Đúng 0
Bình luận (0)
Bài 3: Cho tam giác đều ABC, D là điểm bất kì trên cạnh BC. So sánh độ dài các cạnh của tam giác ABD.
tóm tắt luôn : cạnh BD ngắn hơn các cạnh AB và AD vì nó nằm trên cạnh BC nên sẽ bị giảm độ dài
Đúng 0
Bình luận (0)
Cho tam giác ABC. M la trung điểm của cạnh AB, điểm N thuộc cạnh AC sao cho AN=1/3 AC, MC cắt BN tại O.1:So sánh diện tích tam giác AMC với ABC; ABN với BMC, 2. Biết diện tích tam giác BMO là 30 cm2, tính diện tích tam giác AON và ABC?
Cho tam giác ABC vuông ở A, có cạnh AB=40cm, AC=60cm. M là 1 điểm thuộc cạnh AB sao cho AM=MB, N là 1 điểm thuộc cạnh BC sao cho BN=NC.
a, Tính diện tích các tam giác BMC, ANB.
b, Tính diện tích tứ giác AMNC.
c, Gọi O là điểm cắt nhau của 2 đoạn thẳng AN và CM. So sánh diện tích các tam giác AMO và CNO
\(S_{BMC_{ }_{ }}=\frac{BM.CA}{2}=\frac{20.60}{2}=600cm^2\)
Ta có MN là đường tb của tam giác ABC => MN//AC và MN.2 = AC
=> MN là đường cao của AB ,MN=30 cm
=> SABN=30.40:2=600cm2
b)SAMNC=(MN+AC) .AM:2=(30+60).20:2=900cm2
c)SMAC=MA.AC:2
SANC=CA.MA:2
=> SMAC=SANC=>SAMO=SCON
Đúng 0
Bình luận (0)
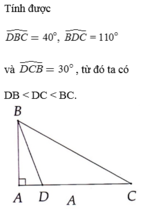
Cho tam giác ABC có A ^ = 90 ° , B ^ = 30 ° . Điểm D thuộc cạnh AC sao cho A B D ^ = 20 ° . So sánh các độ dài các cạnh của tam giác BDC.
cho 1 tam giác ABC vuông TẠI A có cạnh AB = 40 cm , AC = 60 cm . M là một điểm thuộc cạnh AB sao cho AM = MB , N là một điểm thuộc cạnh AB sao cho BN = NC
a, Tính diện tích các tam giác BMC và ANB
b,Tính diện tích tứ giác AMNC
c, Gọi O là điểm gặp nhau của 2 đoạn thẳng AN và CM. So sánh diện tích của tam giác AMO và CNO
a) Ta thấy chiều cao hạ từ C xuống đường thẳng AD là CA. Vậy thì
\(S_{BMC}=\frac{1}{2}.MB.CA=\frac{1}{2}.\frac{AB}{2}.AC=\frac{40.60}{4}=600\left(cm^2\right)\)
Ta thấy chiều cao hạ từ A xuống BC là AH. Vậy thì \(\frac{S_{ANB}}{S_{ABC}}=\frac{\frac{1}{2}.BN.AH}{\frac{1}{2}.BC.AH}=\frac{1}{2}\)
\(S_{ABC}=\frac{1}{2}.40.60=1200\left(cm^2\right)\Rightarrow S_{ANB}=600\left(cm^2\right)\)
b) Ta thấy tam giác BMN và tam giác ANB có chung chiều cao. Vậy \(\frac{S_{BMN}}{S_{ANB}}=\frac{MB}{AB}=\frac{1}{2}\Rightarrow S_{BMN}=600:2=300\left(cm^2\right)\)
Từ đó ta có \(S_{AMNC}=S_{ABC}-S_{BMN}=1200-300=900\left(cm^2\right)\)
c) Ta thấy tam giác MNC và tam giác BMN có chung chiều cao và đáy bằng nhau. Vậy diện tích của chúng bằng nhau.
Tam giác MNA và BMN cũng có chung chiều cao, đáy bằng nhau, vậy diện tích của chúng cũng bằng nhau.
Từ đây suy ra \(S_{MNA}=S_{MNC}\Rightarrow S_{AMO}+S_{MON}=S_{CNO}+S_{MON}\Rightarrow S_{AMO}=S_{CNO}.\)
Đúng 0
Bình luận (0)
Cho hình thang ABCD có đáy CD = AB, hai đường chéo AC và BD cắt nhau tại I. Biết tổng diện tích 2 tam giác AID và BIC là 9,1 cm2. a) So sánh diện tích 2 tam giác AID và BIC.
b) Tính diện tích hình thang ABCD
cho tam giác ABC vuông tại A, có AB=9cm,BC=15cm
a) Tính độ dài AC
b) So sánh các cạnh của tam giác abc, từ đó so sanh các góc của tam giác ABC
c) Trên tia đối của AB lấy điểm D sao cho A là trung điểm của đoạn thẳng BD. Chứng minh tam giác BCD cân
d) Gjoi K là trung điểm của cạnh BC. Đường thẳng DK cắt cạnh AC tại M. Tính độ dài MC
áp dụng định lý Pi-ta-go vào tam giác ABC vuông tại A có:
\(BC^2=AB^2+AC^2\)
\(BC^2-AB^2=AC^2\)
\(15^2-9^2=AC^2\)
\(144=AC^2\)
\(AC=12\)(cm)
b)Có BC<AC<AB
=>A<B<C
c) xét tam giác CAB và tam giác CAD có :
CA chung
DA=AB
góc CAB= gócCAD=90 độ
=>tam giác CAB=tam giác CAD(2 cạnh góc vuông)
=>CB=CD(2 cạnh tương ứng )
=>tam giác BCD cân
d) vì A là trung điểm BD=>DA=DB=>CA là đường trung tuyến DB (1)
có K là trung điểm cạnh BC=>KB=KC=\(\frac{1}{2}\)BC=\(\frac{15}{2}\)=7,5 (cm) (2)
Từ (1) và(2)=>CA =CK=7,5(cm)(trong 1 tam giác vuông đường trung tuyến bằng 1 nửa cạnh huyền)
Từ (1) =>CM=\(\frac{2}{3}\)CA
=>CM=\(\frac{2}{3}\times7,5\)
=>CM=5(cm)
Đúng 0
Bình luận (0)