Giá trị nhỏ nhất của hàm số sau trên khoảng (0; π/2) là:
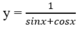
A. 1 B. 2 2
C. - 2 D. 2/ 2
PB
Những câu hỏi liên quan
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:a) 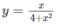trên khoảng (−
∞
;+
∞
);b) trên khoảng
Đọc tiếp
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:
a) 
trên khoảng (−
∞
;+
∞
);
b)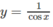 
trên khoảng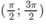 
a)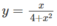 
trên khoảng (−
∞
;+
∞
);
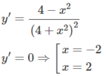
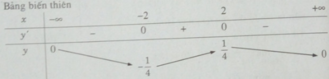
Từ đó ta có min f(x) = −1/4; max f(x) = 1/4
b)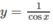 
trên khoảng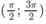 
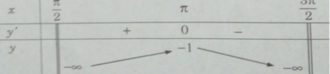
y′ = 0 ⇔ x = π
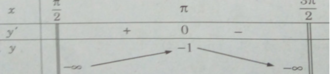
Hàm số không có giá trị nhỏ nhất. Giá trị lớn nhất của hàm số là: max y = y(π) = −1.
Đúng 0
Bình luận (0)
Tìm giá trị lớn nhất và nhỏ nhất của các hàm số sau trên các khoảng, đoạn tương ứng: f(x) = x – ln x + 3 trên khoảng (0; ∞ )
min f(x) = f(1) = 4. Không có giá trị lớn nhất.
Đúng 0
Bình luận (0)
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau: y = x 4 + x 2 trên khoảng (− ∞ ;+ ∞ )
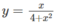trên khoảng (−
∞
;+
∞
);
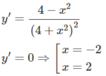
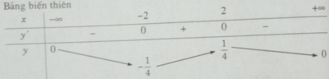
Từ đó ta có min f(x) = −1/4; max f(x) = 1/4
Đúng 0
Bình luận (0)
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:
y
1
cosx
trên khoảng
π
2
;
3
π
2
Đọc tiếp
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau: y = 1 cosx trên khoảng π 2 ; 3 π 2
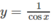trên khoảng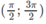 
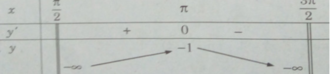
y′ = 0 ⇔ x = π
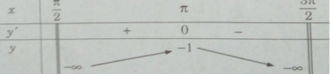
Hàm số không có giá trị nhỏ nhất. Giá trị lớn nhất của hàm số là: max y = y( π ) = −1
Đúng 0
Bình luận (0)
Tìm giá trị nhỏ nhất của hàm số
y
x
+
x
4
trên khoảng
(
0
;
+
∞
)
A.
m
i
n
0
;
+
∞
y
2
B.
m
i
n...
Đọc tiếp
Tìm giá trị nhỏ nhất của hàm số y = x + x 4 trên khoảng ( 0 ; + ∞ )
A. m i n 0 ; + ∞ y = 2
B. m i n 0 ; + ∞ y = 4
C. m i n 0 ; + ∞ y = 0
D. m i n 0 ; + ∞ y = 3
Tìm giá trị nhỏ nhất của hàm số
y
x
2
+
2
x
trên khoảng
(
0
;
+
∞
)
A. không tồn tại B.
m
i
n
y
(
0
;
+
∞
)
3
C. ...
Đọc tiếp
Tìm giá trị nhỏ nhất của hàm số y = x 2 + 2 x trên khoảng ( 0 ; + ∞ )
A. không tồn tại
B. m i n y ( 0 ; + ∞ ) = 3
C. m i n y ( 0 ; + ∞ ) = 1
D. m i n y ( 0 ; + ∞ ) = - 1
Tìm giá trị nhỏ nhất m của hàm số
y
x
3
+
3
x
trên khoảng
0
;
+
∞
A.
m
4
3
4
B.
m
2
3
C.
m
4
D. m...
Đọc tiếp
Tìm giá trị nhỏ nhất m của hàm số y = x 3 + 3 x trên khoảng 0 ; + ∞
A. m = 4 3 4
B. m = 2 3
C. m = 4
D. m = 2
Giá trị nhỏ nhất của hàm số
f
(
x
)
x
+
1
x
trên khoảng
0
;
+
∞
là A.1/2 B.
2
C. 2 D.
2
2
Đọc tiếp
Giá trị nhỏ nhất của hàm số f ( x ) = x + 1 x trên khoảng 0 ; + ∞ là
A.1/2
B. 2
C. 2
D. 2 2
Để giá trị nhỏ nhất của hàm số
y
x
+
1
x
-
m
trên khoảng (0;+∞) bằng –3 thì giá trị của tham số m là: A.
m
11
2
B.
m
1...
Đọc tiếp
Để giá trị nhỏ nhất của hàm số y = x + 1 x - m trên khoảng (0;+∞) bằng –3 thì giá trị của tham số m là:
A. m = 11 2
B. m = 19 3
C. m = 5
D. m = 7
Đáp án C.
Phương pháp: Sử dung BĐT Cauchy.
Cách giải: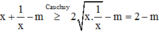 
Đúng 0
Bình luận (0)