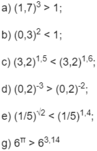Sử dụng tính chất đồng biến, nghịch biến của hàm số mũ, hãy so sánh mỗi cặp số sau: 3 , 2 1 , 5 và 3 , 2 1 , 6
PB
Những câu hỏi liên quan
Sử dụng tính chất đồng biến, nghịch biến của hàm số mũ, hãy so sánh mỗi cặp số sau: 0 , 2 - 3 và 0 , 2 - 2
Sử dụng tính chất đồng biến, nghịch biến của hàm số mũ, hãy so sánh mỗi cặp số sau:

Sử dụng tính chất đồng biến, nghịch biến của hàm số mũ, hãy so sánh mỗi cặp số sau: 1 , 7 3 và 1
Sử dụng tính chất đồng biến, nghịch biến của hàm số mũ, hãy so sánh mỗi cặp số sau: 6 π và 6 3 , 14
Sử dụng tính chất đồng biến, nghịch biến của hàm số mũ, hãy so sánh mỗi cặp số sau: 0 , 3 2 và 1
Sử dụng tính chất đồng biến, nghịch biến của hàm số mũ, hãy so sánh mỗi cặp số sau: 1 / 5 2 và 1 / 5 1 , 4
Vẽ đồ thị của các hàm số \(y=3x+1\) và \(y=-2x^2\). Hãy cho biết:
a) Hàm số \(y=3x+1\) đồng biến hay nghịch biến trên R.
b) Hàm số \(y=-2x^2\) đồng biến hay nghịch biến trên mỗi khoảng: \(\left(-\infty;0\right)\) và \(\left(0;+\infty\right)\)
Vẽ đồ thị \(y = 3x + 1;y = - 2{x^2}\)

a) Trên \(\mathbb{R}\), đồ thị \(y = 3x + 1\) đi lên từ trái sang phải, như vậy hàm số \(y = 3x + 1\) đồng biến trên \(\mathbb{R}\)
b) Trên khoảng \(\left( { - \infty ;0} \right)\), đồ thị \(y = - 2{x^2}\)đi lên từ trái sang phải với mọi \(x \in \left( { - \infty ;0} \right)\) , như vậy hàm số đồng biến trên \(\left( { - \infty ;0} \right)\)
Trên khoảng \(\left( {0; + \infty } \right)\), đồ thị \(y = - 2{x^2}\)đi xuống từ trái sang phải với mọi \(x \in \left( {0; + \infty } \right)\) , như vậy hàm số nghịch biến trên \(\left( {0; + \infty } \right)\)
Đúng 0
Bình luận (0)
Bài 1 : Cho hàm số y=(m-3)x+4 . Với giá trị nào của m thì hàm số đồng biến, nghịch biến Bài 4: Cho hàm số y=(3-√2) x+1 a, Hàm số đồng biến hay nghịch biến? Vì sao? b, Tính các giá trị tương ứng của y khi x nhân các giá trị sau ; O, 1, √2, 3+√2, 3-√2
Bài 1:
Hàm số y=(m-3)x+4 đồng biến trên R khi m-3>0
=>m>3
Hàm số y=(m-3)x+4 nghịch biến trên R khi m-3<0
=>m<3
Bài 4:
a: Vì \(a=3-\sqrt{2}>0\)
nên hàm số \(y=\left(3-\sqrt{2}\right)x+1\) đồng biến trên R
b: Khi x=0 thì \(y=0\left(3-\sqrt{2}\right)+1=1\)
Khi x=1 thì \(y=\left(3-\sqrt{2}\right)\cdot1+1=3-\sqrt{2}+1=4-\sqrt{2}\)
Khi \(x=\sqrt{2}\) thì \(y=\left(3-\sqrt{2}\right)\cdot\sqrt{2}+1=3\sqrt{2}-2+1=3\sqrt{2}-1\)
Khi \(x=3+\sqrt{2}\) thì \(y=\left(3-\sqrt{2}\right)\left(3+\sqrt{2}\right)-1\)
=9-4-1
=9-5
=4
Khi \(x=3-\sqrt{2}\) thì \(y=\left(3-\sqrt{2}\right)^2-1\)
\(=11-6\sqrt{2}-1=10-6\sqrt{2}\)
Đúng 0
Bình luận (0)
Hoạt động 5
Quan sát Hình 11 và nêu nhận xét về tính đồng biến, nghịch biến của hàm số mũ \(y = {\left( {\frac{1}{2}} \right)^x}\). Từ đó, hãy tìm x sao cho \({\left( {\frac{1}{2}} \right)^x} > 2\)
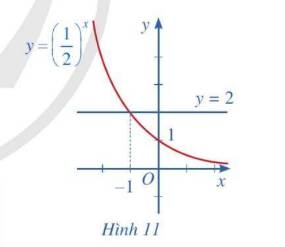
Do \(\dfrac{1}{2}< 1\) ⇒ Hàm số \(y=\left(\dfrac{1}{2}\right)^x\) nghịch biến trên R.
\(\left(\dfrac{1}{2}\right)^x>2\\ \Rightarrow x< log_{\dfrac{1}{2}}2\\ \Rightarrow x< -1\)
Đúng 0
Bình luận (0)