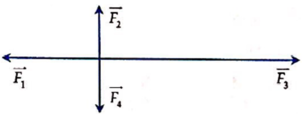
Một chất điểm chịu tác dụng của bốn lực đồng phẳng F 1 → ; F 2 → ; F 3 → ; F 4 → . Biết độ lớn của các lực là F = 2N, F2 = 3N, F3 = 6N. Tìm độ lớn của hợp lực tác dụng lên chất điểm.
A. 14 N.
B. 10 N.
C. 4 N.
D. 6 N.
Một chất điểm chịu tác dụng đồng thời của hai lực thành phần có độ lớn F 1 v à F 2 thì hợp lực F của chúng luôn có độ lớn thỏa mãn hệ thức:
A. F = F 1 2 + F 2 2
B. F 1 − F 2 ≤ F ≤ F 1 + F 2
C. F = F 1 + F 2
D. F = F 1 2 + F 2 2
Một chất điểm chịu tác dụng đồng thời của hai lực thành phần có độ lớn F 1 v à F 2 thì hợp lực F của chúng luôn có độ lớn thỏa mãn hệ thức:
A. F = F 1 2 + F 2 2
B. F 1 − F 2 ≤ F ≤ F 1 + F 2
C. F = F 1 + F 2
D. F = F 1 2 + F 2 2
Câu 11: Một chất điểm chịu tác dụng của đồng thời hai lực cùng độ lớn 20N, góc hợp bởi hai lực là 120o. Hợp của hai lực trên
A. F = 20N; ( F➝ ; F1 ➝ ) = 60o
B. F = 20√3 N; ( F➝ ; F1 ➝ ) = 60o
C. F = 20N; ( F➝ ; F1 ➝ ) = 120o
D. F = 20√3 N; ( F➝ ; F1 ➝ ) = 120o
Câu 11: Một chất điểm chịu tác dụng của đồng thời hai lực cùng độ lớn 20N, góc hợp bởi hai lực là 120o. Hợp của hai lực trên
A. F = 20N; ( F➝ ; F1 ➝ ) = 60o
B. F = 20√3 N; ( F➝ ; F1 ➝ ) = 60o
C. F = 20N; ( F➝ ; F1 ➝ ) = 120o
D. F = 20√3 N; ( F➝ ; F1 ➝ ) = 120o
một chất điểm chịu tác dụng đồng thời hai lực đồng quy có giá vuông góc nhau và có độ lớn lần lượt là 3N và 4N độ lớn hợp lực F là
A,25N B.7N C.5N .D1N
một chất điểm chịu tác dụng đồng thời hai lực đồng quy có giá vuông góc nhau và có độ lớn lần lượt là 3N và 4N độ lớn hợp lực F là
A,25N B.7N C.5N .D1N
Một chất điểm dụng yên khi chịu tác dụng đồng thời của 3 lực 3N;4Nva5N.Tìm góc hợp bởi 2luc3N va4N.
Chất điểm đứng yên khi hợp lực tác dụng lên nó bằng 0
\(\vec{F_1}+\vec{F_2}+\vec{F_3}=\vec{0}\)
Đặt \(\vec{F_{12}}=\vec{F_1}+\vec{F_2}\) suy ra \(\vec{F_{12}}+\vec{F_3}=\vec{0}\)
\(\Rightarrow F_{12}=F_3=5N\)
Do \(3^2+4^2=5^2\)
nên \(\vec{F_1}\perp\vec{F_2}\)
Vậy góc tạo bởi hai lực 3N và 4N là 900
Một chất điểm chịu tác dụng của lực F = 2N bắt đầu chuyển động. Sau 2 giây đi được 2 m. Tính khối lượng chất điểm.
Ta có :
\(S=v_0t+\frac{1}{2}at^2\)
\(\Rightarrow\text{ }2=0+\frac{1}{2}a\cdot2^2\)
\(\Rightarrow\text{ }a=1\text{ m/s}^2\)
\(m=\frac{F}{a}=\frac{2}{1}=2\text{ kg}\)
Một chất điểm chịu tác dụng của hai lực. Để chất điểm cân bằng thì hai lực phải
A. cùng giá, cùng chiều, cùng độ lớn.
B. cùng giá, ngược chiều, cùng độ lớn.
C. ngược chiều, cùng độ lớn.
D. cùng giá, cùng độ lớn.
Chọn đáp án B
Một chất điểm chịu tác dụng của hai lực. Để chất điểm cân bằng thì hai lực phải cùng giá, ngược chiều, cùng độ lớn.
một chất điểm chịu tác dụng của 3 lực đồng phẳng,đồng quy cso cùng độ lớn 15N .biết góc tạo bới hợp lực (F1,F2)=(F2,F3)=60độ.Tính hợp lực của ba lực này
hợp lực của F1,F2
\(F_{12}=\sqrt{F^2_1+F^2_2+2.F_1.F2.cos60^0}\)=\(15\sqrt{3}\)N
hợp lực của F12 và F3 là
\(F_{123}=\sqrt{F_{12}^2+F_3^3}\)=30N
\(F_{12}=\sqrt{F_1^2+F^2_2+2F_1F_2cos\alpha}=\sqrt{2.15^2+2.15^2.\dfrac{1}{2}}=15\sqrt{3}\left(N\right)\)
\(F_{23}=\sqrt{F_2^2+F^2_3+2F_2F_3cos\alpha}=\sqrt{2.15^2+2.15^2.\dfrac{1}{2}}=15\sqrt{3}\left(N\right)\)
Hợp lực của 3 lực này là:
\(F_{123}=\sqrt{F_1^2+F^2_2+2F_1F_2cos\alpha}=\sqrt{2\left(15\sqrt{3}\right)^2+2.\left(15\sqrt{3}\right)^2.\dfrac{-1}{2}}=15\sqrt{3}\left(N\right)\)
Một chất điểm chịu tác dụng của 2 lực, chất điểm ấy cân bằng khi:
A. Hai lực ngược hướng, cùng độ lớn.
B. Hai lực cùng hướng, cùng độ lớn
C. Hai lực cùng độ lớn, cùng chiều
D. Hai lực cùng độ lớn, ngược chiều
Ta có: Hai lực được gọi là cân bằng khi chúng có cùng phương, ngược chiều và cùng độ lớn
⇒ Chất điểm ấy cân bằng khi hai lực ngược hướng (cùng phương, ngược chiều) và có cùng độ lớn.
Đáp án: A