Đáp án B

Ta có: P T ⇔ 4 c os 3 x − 3 cos x + 2 sin 2 x + 9 sin x − 5 = 0  

⇔ cos x 4 c os 2 x − 3 + 2 sin 2 x + 9 sin x − 5 = 0 ⇔ cos x 1 − 4 sin 2 x + 2 sin x − 1 s inx + 5 = 0 ⇔ 2 sin x − 1 cos x + 2 sin x cos x + s inx + 5 = 0 ⇔ 2 sin x − 1 s inx + cos x + sin 2 x + 5 = 0 ⇔ 2 sin x − 1 = 0 ⇔ s inx = 1 2 ⇔ x = π 6 k 2 π x = 5 π 6 + k 2 π

Với x ∈ 0 ; 3 π ⇒ x = π 6 ; 5 π 6 ; π 6 + 2 π ; 5 π 6 + 2 π ⇒ T = 6 π .

Chọn D

Phương trình tương với:

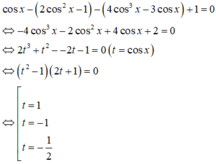
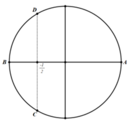
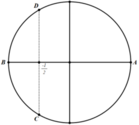
Trên đường tròn đơn vị, các điểm nghiệm của phương trình là 4 điểm A, B, C, D như hình vẽ. Do đó trên nửa khoảng [ - π ; 0 ) , phương trình có đúng 2 nghiệm (là - π  và - 2 π 3 ).

Đáp án D.

Phương trình tương với:

cos x − 2 cos 2 x − 1 − 4 cos 3 x − 3 cos x + 1 = 0 ⇔ − 4 cos 3 x − 2 cos 2 x + 4 cos x + 2 = 0 ⇔ 2 t 3 + t 2 − − 2 t − 1 = 0 t = cos x ⇔ t 2 − 1 2 t + 1 = 0 ⇔ t = 1 t = − 1 t = − 1 2

Trên đường tròn đơn vị, các điểm nghiệm của phương trình là 4 điểm A, B, C, D như hình vẽ. Do đó trên nửa khoảng − π ; 0 , phương trình có đúng 2 nghiệm (là − π  và − 2 π 3 ).

Đáp án B

Chọn D

ta có cos2x - √3sin2x= 1

⇔ 1 2 cos 2x -   3 2 . sin 2 x =    1 2 ⇔ sin   π 6 . c os2x - cos π 6 . sin2x =  1 2 ⇔ sin   π 6 − 2 x  =  sin π 6 ⇔ π 6 − 2 x =    π 6 + ​ k 2 π π 6 − 2 x =    π − π 6 + ​ k 2 π ⇔ x = − k π x =    − π 3 − k π ⇔ x = l π x =    − π 3 + ​ l π ​​       ( l = − k    ∈ Z )

Suy ra phương trình chỉ có một nghiệm thuộc(0;π) là  x   =   2 π 3