Một con lắc lò xo dao động điều hòa với phương trình: x = 4 cos ωt + π 6 c m . Sau thời gian Δ t = 5 , 25 T (T là chu kì dao động) tính từ lúc t = 0, vật đi được quãng đường là:
A. 80,732m
B. 81,462cm
C. 85,464cm
D. 96,836cm
Một con lắc lò xo nằm ngang dao động điều hòa với phương trình x=5cos(10πt+π/3)cm. Chiều dài tự nhiên của lò xo là 20cm. Tính lmax,lmin của lò xo trong quá trình vật dao động.
\(l_{max}=l_0+\Delta l+A\Rightarrow\left\{{}\begin{matrix}A=5cm=0,02m\\\Delta l=\dfrac{g}{\omega^2}=\dfrac{10}{\left(10\right)^2}=0,1m\\l_0=0,2m\end{matrix}\right.\)
=> \(l_{max}=0,2+0,1+0,02=0,32\left(m\right)=32cm\)
\(l_{min}=l_0+\Delta l-A=0,2+0,1-0,02=0,28\left(m\right)=28\left(cm\right)\)
Vậy ...
Một con lắc lò xo dao động điều hòa trên trục Ox với phương trình dao động x = Acos(ωt – π/6). Gọi Wd, Wt lần lượt là động năng, thế năng của con lắc. Trong một chu kì Wd ≥ Wt là 1/3 s. Thời điểm vận tốc v và li độ x của vật thỏa mãn v = ω|x| lần thứ 2016 kể từ thời điểm ban đầu là
A. 703,59 s.
B. 1007,958 s.
C. 503,71 s.
D. 2014,21 s.
Một con lắc lò xo dao động điều hòa trên trục Ox với phương trình dao động x = Acos(ωt – π/6). Gọi Wđ, Wt lần lượt là động năng, thế năng của con lắc. Trong một chu kì Wđ ≥ Wt là 1/3 s. Thời điểm vận tốc v và li độ x của vật thỏa mãn v = ω|x| lần thứ 2016 kể từ thời điểm ban đầu là:
A. 503,71 s.
B. 1007,958 s.
C. 2014,21 s.
D. 703,59 s.
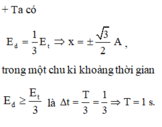
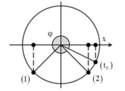
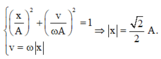
+ Tại t=0, vật đi qua vị trí x = 3 2 A , theo chiều dương. Biểu diễn các vị trí tương ứng trên đường tròn.
+ Trong một chu kì vật đi qua vị trí thỏa mãn yêu cầu bài toán 2 lần → tách 2016 = 2014+2
Vậy tổng thời gian là
![]()
Đáp án B
Một con lắc lò xo dao động điều hòa trên trục Ox với phương trình dao động x = A cos ( ω t – π / 6 ) . Gọi W d , W t lần lượt là động năng, thế năng của con lắc. Trong một chu kì W d ≥ W t là 1/3 s. Thời điểm vận tốc v và li độ x của vật thỏa mãn v = ω | x | lần thứ 2016 kể từ thời điểm ban đầu là
A. 703,59 s
B. 1007,958 s
C. 503,71 s
D. 2014,21 s
Một con lắc lò xo dao động điều hòa trên trục Ox với phương trình dao động x = Acos(ωt – π/6). Gọi W đ , W t lần lượt là động năng, thế năng của con lắc. Trong một chu kì W đ ≥ W t là 1/3 s. Thời điểm vận tốc v và li độ x của vật thỏa mãn v = ω|x| lần thứ 2016 kể từ thời điểm ban đầu là:
A. 503,71 s.
B. 1007,958 s
C. 2014,21 s.
D. 703,59 s.
Đáp án B
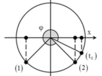
+ Ta có
E d = 1 3 E t ⇒ x = ± 3 2 A
trong một chu kì khoảng thời gian E d ≥ E t 3 là Δ t = T 3 = 1 3 ⇒ T = 1 s .
+ Kết hợp với: x A 2 + v ω A 2 = 1 v = ω x ⇒ x = 2 2 A .
+ Tại t=0, vật đi qua vị trí x = 3 2 A theo chiều dương. Biểu diễn các vị trí tương ứng trên đường tròn
+ Trong một chu kì vật đi qua vị trí thỏa mãn yêu cầu bài toán 2 lần->2016=2014+2
Vậy tổng thời gian là Δ t = t φ + 1007 T = 23 24 + 1007 = 1007 , 958 s .
Một con lắc lò xo dao động điều hòa có phương trình x =10cos(20t + π)(x tính bằng cm, t tính bằng s). Con lắc này dao động với tần số góc là
A. 10 rad/s
B. 20 rad/s
C. 5 rad/s
D. 15 rad/s
Đáp án B
Tần số góc của dao động ω = 20 rad/s
Một con lắc lò xo dao động điều hòa có phương trình x =10cos(20t + π)(x tính bằng cm, t tính bằng s). Con lắc này dao động với tần số góc là
A. 10 rad/s .
B. 20 rad/s.
C. 5 rad/s.
D. 15 rad/s.
Đáp án B
HD: Tần số góc của dao động 20 rad/s
Một con lắc lò xo đang dao động điều hòa với phương trình x = A cos ( ω t ) Người ta thấy cứ sau 0,5(s) động năng lại bằng thế năng thì tần số góc dao động của con lắc sẽ là:
A. π r a d / s
B. 0 , 5 π r a d / s
C. 4 π r a d / s
D. 2 π r a d / s
Đáp án A.
Trong dao động điều hòa, cứ T/4 thì động năng lại bằng thế năng
Theo đó ta có
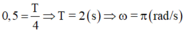
Con lắc lò xo nằm ngang gồm lò xo có độ cứng k, dao động điều hòa với phương trình x = Acos(ωt + φ). Độ lớn cực đại của lực kéo về tác dụng lên con lắc là :
A. kA
B. k 2 A
C. k A
D. k A 2
Đáp án A
+ Độ lớn cực đại của lực kéo về F m a x = k A
Con lắc lò xo nằm ngang gồm lò xo có độ cứng k, dao động điều hòa với phương trình x = Acos(ωt + φ). Độ lớn cực đại của lực kéo về tác dụng lên con lắc là :
A. kA.
B. k2A.
C. k A
D. kA2.