Vẽ đồ thị của các hàm số sau và xét tính chẵn lẻ của chúng
y = 5
PB
Những câu hỏi liên quan
Vẽ đồ thị của các hàm số sau và xét tính chẵn lẻ của chúng
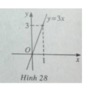
y = 3x
Đồ thị là hình 28. Hàm số là hàm số lẻ.
Đúng 0
Bình luận (0)
Vẽ đồ thị của các hàm số sau và xét tính chẵn lẻ của chúng
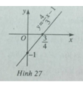
y = (4x / 3) - 1
Đồ thị là hình 27. Hàm số không là hàm số chẵn, không là hàm số lẻ.
Đúng 0
Bình luận (0)
Vẽ đồ thị của các hàm số sau và xét tính chẵn lẻ của chúng
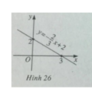
y = (-2x / 3) + 2
Đồ thị là hình 26. Hàm số không là hàm số chẵn, không là hàm số lẻ
Đúng 0
Bình luận (0)
Vẽ đồ thị của các hàm số sau và xét tính chẵn lẻ của chúng ?
a) \(y=-\dfrac{2}{3}x+2\)
b) \(y=\dfrac{4}{3}x-1\)
c) \(y=3x\)
d) \(y=5\)
e) \(y=\sqrt{2}-1\)
Vẽ trên cùng một hệ trục tọa độ đồ thị của các hàm số sau và nêu nhận xét về tập xác định của chúng: y = x 2 , y = x 1 2 , y = x - 1
Xét các hàm số sau và đồ thị của chúng:
y = -x2/2 (H.4a)
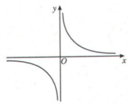
Xét dấu đạo hàm của mỗi hàm số và điền vào bảng tương ứng.
Xét tính chẵn lẻ của các hàm số sau: y = |x|
Đặt y = f(x) = |x|.
+ Tập xác định D = R nên với ∀ x ∈ D thì –x ∈ D.
+ f(–x) = |–x| = |x| = f(x).
Vậy hàm số y = |x| là hàm số chẵn.
Đúng 0
Bình luận (0)
LH
13 tháng 9 2015 lúc 10:52
Cho các hàm số \(y=f\left(x\right)=2x\) và \(y=g\left(x\right)=\frac{18}{x}\). Không vẽ đồ thị của chúng, em hãy tính tọa độ giao điểm của 2 đồ thị, sau đó rút ra nhận xét về phương pháp chung để tìm tọa độ giao điểm của 2 đồ thị hàm số.
Gọi A (xo; yo) là giao điểm của hai đồ thị
A \(\in\) đồ thị hàm số y = 2x => yo = 2xo
A \(\in\) đồ thị hàm số y = 18/x => yo = 18/xo
=> 2xo = 18/xo => 2xo2 = 18 <=> x2o = 9 => xo = 3 hoặc xo = - 3
+) xo = 3 => yo = 6 => A (3;6)
+) xo = -3 => yo = - 6 => A (-3; -6)
Vậy...
* Nhận xét: Để tìm tọa độ giao điểm của hai đồ thị hàm số
- Tìm hoành độ giao điểm :Giải f(x) = g(x) => x = ....
- Thay x tìm được vào hàm số y = f(x) hoặc y = g(x) => y =...
Đúng 0
Bình luận (0)
Xét tính chẵn lẻ của các hàm số sau: y = x3 + x
Đặt y = f(x) = x3 + x.
+ TXĐ: D = R nên với ∀x ∈ D thì –x ∈ D.
+ f(–x) = (–x)3 + (–x) = –x3 – x = – (x3 + x) = –f(x)
Vậy y = x3 + x là một hàm số lẻ.
Đúng 0
Bình luận (0)