Tìm tất cả các giá trị thực của tham số m sao cho hàm số y = 1 3 x 3 - 1 2 m x 2 + 2 m x - 3 m + 4 nghịch biến trên một đoạn có độ dài là 3?
A. m=-1;m=9
B. m=-1
C. m=9
D. m=1;m=-9
Tìm tất cả các giá trị thực của tham số m sao cho hàm số y = ( m - 3 ) x - ( 2 m + 1 ) cos x luôn nghịch biến trên ℝ ?
A. - 4 ≤ m ≤ 2 3
B. m ≥ 2
C. m > 3 m ≠ 1
D. m ≤ 2
Câu 1 : Tìm tất cả các giá trị của tham số thực m để hàm số \(y=mx^3-2mx^2+\left(m-2\right)x+1\) không có cực trị
Câu 2: Tìm tất cả các giá trị thực của tham số m để hàm số \(y=\left(m-1\right)x^4-2\left(m-3\right)x^2+1\) không có cực đại
Tìm tất cả các giá trị thực của tham số m sao cho hàm số y= (m-3)x- (2m+1).cos x luôn nghịch biến trên R?
A. - 4 ≤ m ≤ 2 3
B. m> 2
C. m > 3 m ≠ 1
D. m<2
Chọn A.
Tập xác định:D= R. Ta có:y ‘= m-3 + (2m+1).sinx
Hàm số nghịch biến trên R
![]()
Trường hợp 1: m= -1/ 2 ; ta có 0 ≤ 7 2 ∀ x ∈ ℝ
Vậy hàm số luôn nghịch biến trên R.
Trường hợp 2: m< -1/ 2 ; ta có
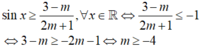
Trường hợp 3:m > -1/2 ; ta có:
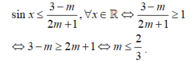
Vậy - 4 ≤ m ≤ 2 3
Câu 3 Để đồ thị hàm số \(y=-x^4-\left(m-3\right)x^2+m+1\) có điểm cực đạt mà không có điểm cực tiểu thì tất cả giá trị thực của tham số m là
Câu 4 Cho hàm số \(y=x^4-2mx^2+m\) .Tìm tất cả các giá trị thực của m để hàm số có 3 cực trị
tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số \(y=\dfrac{5x-3}{x^2-2mx+1}\) không có tiệm cận đứng .
Do mẫu có bậc 2 còn tử bậc 1 \(\Rightarrow\)hàm không có tiệm cận đứng khi và chỉ khi phương trình \(x^2-2mx+1=0\) vô nghiệm
\(\Leftrightarrow\Delta'=m^2-1< 0\)
\(\Rightarrow-1< m< 1\)
Tìm tất cả các giá trị thực của tham số m sao cho hàm số y = x 4 - 2 n - 1 x 2 + m - 2 đồng biến trên khoảng (1; 3)?
A. m ∈ [ - 5 ; 2 )
B. m ∈ ( - ∞ ; 2 ]
C. m ∈ 2 ; + ∞
D. m ∈ - ∞ ; - 5
Chọn B.
Tập xác định D = R.

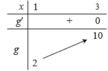
Dựa vào bảng biến thiên, kết luận: m ≤ min g(x) ⇔ m ≤ 2
Tìm tất cả các giá trị thực của tham số m sao cho đồ thị hàm số y = 2 x - 3 ( m - 1 ) x 2 + 4 có tiệm cận ngang
A. m > 0
B. m ≥ 1
C. m > 1
D. Không có giá trị nào của m
Ta có
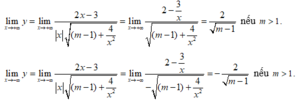
Vậy với m > 1 thì đồ thị hàm số 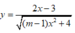 có hai tiệm cận ngang là
có hai tiệm cận ngang là 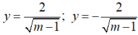
Chọn đáp án C.
Tìm tổng tất cả các giá trị thực của tham số m sao cho đường thẳng đi qua hai điểm cực trị của đồ thị hàm số y = 2 x 3 + 3 ( m - 1 ) x 2 + 6 m ( 1 - 2 m ) x song song đường thẳng y= -4x.
![]()
![]()
![]()
![]()
Tìm tất cả các giá trị thực của tham số m sao cho hàm số y = x - m + 2 x + 1 giảm trên các khoảng mà nó xác định ?
A. m < - 3.
B. m ≤ - 3.
C. m ≤ 1.
D. m < 1 .
Tìm tất cả các giá trị thực của tham số m sao cho hàm số y = x - m + 2 x + 1 giảm trên các khoảng mà nó xác định ?
A. m < 1
B. m ≤ -3
C. m ≤ 1
D. m < -3
Chọn A
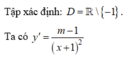
Để hàm số giảm trên các khoảng mà nó xác định
![]()