Tìm số phức z thỏa mãn:
|z − (2 + i)| = 10 và z ¯ .z = 25
Tìm số phức z thỏa mãn:
|z − (2 + i)| = 10 và z z = 25
Đặt z = x + yi. Từ điều kiện của đầu bài ta được:
x - 2 2 + y - 1 2 = 10 và x 2 + y 2 = 25
Đáp số: z = 5 và z = 3 + 4i
Tìm các số phức z thỏa mãn: z - ( 2 + i ) = 10 và z . z ¯ = 25
![]()
![]()
![]()
![]()
Tìm các số phức z thỏa mãn: z - 2 + i = 10 và z . z ¯ = 25
A. z 1 = - 5 ; z 2 = - 3 + 4 i
B. z 1 = 5 ; z 2 = 3 - 4 i
C. z 1 = 5 ; z 2 = 3 + 4 i
D. z 1 = - 5 ; z 2 = - 3 - 4 i
Tìm số phức z thỏa mãn hệ thức z - 2 + i = 10 v à z . z ¯ = 25
A. z = 3 + 4i; z = 5.
B. z = 3 + 4i; z= -5.
C. z = -3 + 4i;z = 5.
D. z = 3 - 4i; z = -5.
Chọn A.
![]()
⇒ z ¯ = a - b i

![]()
![]()
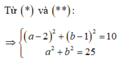
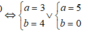
Vậy có hai số phức thỏa mãn là: z = 3+ 4i hoặc z = 5.
Biết số phức z có phần ảo khác 0 và thỏa mãn z - ( 2 + i ) = 10 v à z . z ¯ = 25 . Điểm nào sau đây biểu diễn số phức z trên?
![]()
![]()
![]()
![]()
Xét các số phức z thỏa mãn z + 1 - i + z - 3 + i = 2 5 . Tìm giá trị nhỏ nhất của P = z + 2 + 4 i .
A. P m i n = 11 5 5
B. P m i n = 2 + 2
C. P m i n = 5
D. P m i n = 5 - 2
Tìm số phức \(z\) thỏa mãn \(\left|z-\left(2+i\right)\right|=\sqrt{10}\) và \(z\overline{z}=25\)
Giải:
Đặt \(z=a+bi(a,b\in\mathbb{R})\)
Theo bài ra ta có:
\(\left\{\begin{matrix} |(a-2)+i(b-1)|=\sqrt{10}\\ z\overline{z}=|z|^2=a^2+b^2=25\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} (a-2)^2+(b-1)^2=10\\ a^2+b^2=25\end{matrix}\right.\)
\(\left\{\begin{matrix} 2a+b=10\\ a^2+b^2=25\end{matrix}\right.\Rightarrow a^2+(10-2a)^2=25\rightarrow a=5\) hoặc \(a=3\)
\(\Rightarrow b=0;4\)
Vậy \(z\in \left \{5,3+4i\right\}\)
Tìm số phức z thỏa mzãn hệ thức z - 2 + i = 10 và z . z ¯ = 25
A. z = 3 + 4i; z = 5.
B. z = 3 + 4i; z = -4.
C. z = -3 + 4i; z = 5.
D. z = 3 - 4i; z = -5.
Chọn A.
Gọi z = a + bi khi đó ![]()
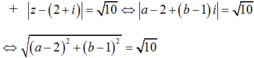
Hay (a – 2)2 + (b – 1)2 = 10
![]()
Từ (*) và (**) 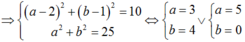
Vậy z = 3 + 4i hoặc z = 5.
Tìm số phức z thỏa mãn |z-2|=|z| và (z+1)( z ¯ - i ) là số thực
A. z = 1 + 2 i
B. z = - 1 - 2 i
C. z = 2 - i
D. z = 1 - 2 i