Cho số phức z có môđun bằng 1. Giá trị nhỏ nhất của biểu thức T = z 2 + 1 z 2 là
A. 2
B. 0
C. -2
D. -1
PB
Những câu hỏi liên quan
Cho số phức z thỏa mãn | z + 1 - i | = | z | . Giá trị nhỏ nhất của môđun của z là
A. 0
B. 1 2
C. 1
D. 1 2
Chọn D
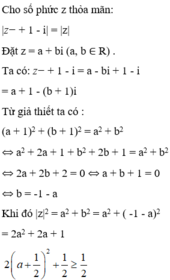
Từ đó suy ra môđun của z nhỏ nhất bằng 1 2
Đúng 0
Bình luận (0)
Tìm số phức z thỏa mãn
|
z
-
1
-
i
|
5
và biểu thức
T
|
z
-
7
-
9
i
|
+
2
|
z
-
8
i
|
đạt giá trị nhỏ nhất
Đọc tiếp
Tìm số phức z thỏa mãn | z - 1 - i | = 5 và biểu thức T = | z - 7 - 9 i | + 2 | z - 8 i | đạt giá trị nhỏ nhất
Cho
z
x
+
y
i
với x, y
∈
R
là số phức thỏa mãn điều kiện
z
¯
+
2
-
3
i
≤
|
z
+
i
-
2
|
≤
5
. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ...
Đọc tiếp
Cho z = x + y i với x, y ∈ R là số phức thỏa mãn điều kiện z ¯ + 2 - 3 i ≤ | z + i - 2 | ≤ 5 . Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P = x 2 + y 2 + 8 x + 6 x . Tính M+m.
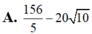
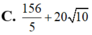
Bài 1:cho ba số x,y,z khác 0 thỏa mãn điều kiện:
y+z-x/x=z+x-y/y=x+y-z/z. Khi đó B= (1+x/y).(1+y+z).(1+z+x) có giá trị bằng.....
Bài 2:Giá trị nhỏ nhất của biểu thức A=(x^2-2x-q).(x^2-2x+3) là.....
GIẢI CHI TIẾT HỘ MÌNH NHÉ
ban sat long nhan natsu oi giai nhu vay thi ai hieu ham
Đúng 0
Bình luận (0)
bài 1
Từ tính chất dãy tỉ số bằng nhau ta có :
\(\frac{y+z-x}{x}=\frac{z+x-y}{y}=\frac{x+y-z}{z}=\frac{y+z-x+z+x-y+x+y-z}{x+y+x}=\frac{x+y+z}{x+y+z}=1\)
=> x=y=z
=> B = 2.2.2 = 8
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Trong các số phức thỏa mãn điều kiện
z
-
4
i
-
2
2
i
-
z
, môđun nhỏ nhất của số phức z bằng: A.
2
B.
3
C.
2
2
D.
2
3
Đọc tiếp
Trong các số phức thỏa mãn điều kiện z - 4 i - 2 = 2 i - z , môđun nhỏ nhất của số phức z bằng:
A. 2
B. 3
C. 2 2
D. 2 3
Cho các số phức z, w thỏa mãn |z+2-2i|=|z-4i|, w=iz+1. Giá trị nhỏ nhất của |w| là
A. 2 2
B. 2
C. 3 2 2
D. 2 2
Cho các số phức z, w thỏa mãn
z
+
2
-
2
i
z
-
4
i
,
w
i
z
+
1
. Giá trị nhỏ nhất cu...
Đọc tiếp
Cho các số phức z, w thỏa mãn z + 2 - 2 i = z - 4 i , w = i z + 1 .
Giá trị nhỏ nhất của w là
A. 2 2
B. 2
C. 3 2 2
D. 2 2
Đáp án A.
Đặt 
,
khi đó 
và 
Nên ta có
Khi đó
Dễ thấy
Đúng 0
Bình luận (0)
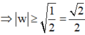
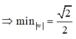
a) Cho x+y=1. Tìm giá trị nhỏ nhất của biểu thức x3+y3
b) Cho 3 số dương x, y, z thỏa mãn điều kiện x+y+z=2. Tìm GTNN của biểu thức: P=\(\frac{x^2}{y+z}+\frac{y^2}{z+x}+\frac{z^2}{y+x}\)
a, Từ x+y=1
=>x=1-y
Ta có: \(x^3+y^3=\left(1-y\right)^3+y^3=1-3y+3y^2-y^3+y^3\)
\(=3y^2-3y+1=3\left(y^2-y+\frac{1}{3}\right)=3\left(y^2-2.y.\frac{1}{2}+\frac{1}{4}+\frac{1}{12}\right)\)
\(=3\left[\left(y-\frac{1}{2}\right)^2+\frac{1}{12}\right]=3\left(y-\frac{1}{2}\right)^2+\frac{1}{4}\ge\frac{1}{4}\) với mọi y
=>GTNN của x3+y3 là 1/4
Dấu "=" xảy ra \(< =>\left(y-\frac{1}{2}\right)^2=0< =>y=\frac{1}{2}< =>x=y=\frac{1}{2}\) (vì x=1-y)
Vậy .......................................
b) Ta có: \(P=\frac{x^2}{y+z}+\frac{y^2}{z+x}+\frac{z^2}{y+x}\)
\(=\left(\frac{x^2}{y+z}+x\right)+\left(\frac{y^2}{z+x}+y\right)+\left(\frac{z^2}{y+z}+z\right)-\left(x+y+z\right)\)
\(=\frac{x\left(x+y+z\right)}{y+z}+\frac{y\left(x+y+z\right)}{z+x}+\frac{z\left(x+y+z\right)}{y+z}-\left(x+y+z\right)\)
\(=\left(x+y+z\right)\left(\frac{x}{y+z}+\frac{y}{z+x}+\frac{z}{y+x}-1\right)\)
Đặt \(A=\frac{x}{y+z}+\frac{y}{z+x}+\frac{z}{y+x}\)
\(A=\left(\frac{x}{y+z}+1\right)+\left(\frac{y}{z+x}+1\right)+\left(\frac{z}{y+x}+1\right)-3\)
\(=\frac{x+y+z}{y+z}+\frac{x+y+z}{z+x}+\frac{x+y+z}{y+x}-3\)
\(=\left(x+y+z\right)\left(\frac{1}{y+x}+\frac{1}{y+z}+\frac{1}{z+x}\right)-3\)
\(=\frac{1}{2}\left[\left(x+y\right)+\left(y+z\right)+\left(z+x\right)\right]\left(\frac{1}{x+y}+\frac{1}{y+z}+\frac{1}{z+x}\right)-3\ge\frac{9}{2}-3=\frac{3}{2}\)
(phần này nhân phá ngoặc rồi dùng biến đổi tương đương)
\(=>P=\left(x+y+z\right)\left(\frac{x}{y+z}+\frac{y}{z+x}+\frac{z}{y+x}-1\right)\ge2\left(\frac{3}{2}-1\right)=1\)
=>minP=1
Dấu "=" xảy ra <=>x=y=z
Vậy.....................
Đúng 0
Bình luận (0)
1. BCNN ( 10 ; 11 ; 12 )2 Nếu -3x -27( x E Z ) thì giá trị của x là .. 3 Số chính phương nhỏ nhất khác 04 Cho 3 số nguyên liên tiếp có tổng bằng 0 số nhỏ nhất trong ba số đó là 5 Giá Trị Biểu Thức 1-2+3-4+....+199-200+100 là ..... 6 Tính A 5.(-3)2 - 14 . (-8) + ( - 57 ) A 7 Số tự nhiên a lớn nhất sao cho ( 3 + 1 )3 -343
Đọc tiếp
1. BCNN ( 10 ; 11 ; 12 )
2 Nếu -3x = -27( x E Z ) thì giá trị của x là ..
3 Số chính phương nhỏ nhất khác 0
4 Cho 3 số nguyên liên tiếp có tổng bằng 0 số nhỏ nhất trong ba số đó là
5 Giá Trị Biểu Thức 1-2+3-4+....+199-200+100 là .....
6 Tính A = 5.(-3)2 - 14 . (-8) + ( - 57 ) A=
7 Số tự nhiên a lớn nhất sao cho ( 3 + 1 )3 = -343
1.660
3.4
4.-1
5.0
6.100
câu 7 ko hiểu, mà nhớ tick nha
Đúng 0
Bình luận (0)
CAU 1=660
CAU 3=4
CAU4=-1
CAU5=0
CAU 6=100
Đúng 0
Bình luận (0)