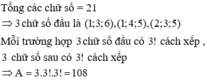có bao nhiêu số tự nhiên có sáu chữ số khác nhau nhỏ hơn 500 000
LN
Những câu hỏi liên quan
Có bao nhiêu số tự nhiên có sáu chữ số khác nhau mà mỗi số đó đều nhỏ hơn 500 000?
Số các số tự nhiên có sáu chữ số khác nhau mà mỗi số đó đều nhỏ hơn 500 000 là..........?
có bao nhiêu số tự nhiên có sáu chữ số khác nhau mà nhỏ hơn 500000
Có 400000 số tự nhiên có sáu chữ số khác nhau mà nhỏ hơn 500000.
Đúng 0
Bình luận (0)
có bao nhiêu số tự nhiên có 6 chữ số khác nhau mà mỗi số nhỏ hơn 400 000?
Từ các chữ số 1, 2, 3, 4, 5, 6 có thể lập được bao nhiêu số tự nhiên, mỗi số gồm sáu chữ số khác nhau và tổng của ba chữ số đầu nhỏ hơn tổng của ba chữ số cuối một đơn vị
A. 108 số.
B. 180 số.
C. 118 số.
D. 181 số.
Từ các chữ số 1,2,3,4,5,6 có thể lập được bao nhiêu số tự nhiên, mỗi số có 6 chữ số và thỏa mãn điều kiện: sáu chữ số của mỗi số là khác nhau và trong mỗi số đó tổng của 3 chữ số đầu nhỏ hơn tổng của ba chữ số cuối một đơn vị.
Ta có 1+2+3+4+5+6+ =21 Vậy tổng của 3 chữ số đầu là 10
Dễ thấy 1+3+6 = 1+4+5 = 2+3+5
Vậy có 3 cách chọn 3 nhóm 3 chữ số đầu (1,3,6 hoặc 1,4,5 hoặc 2,3,5)
Với 1 cách chọn nhóm 3 chữ số thì có 3! cách để lập ra số \(\overline{a_1a_2a_3}\)
Với 3 số còn lại thì có 3! cách để lập ra số \(\overline{a_4a_5a_6}\)
(ở đây \(\overline{a_1a_2a_3a_4a_5a_6}\) là số thỏa mãn yêu cầu đề ra)
Theo quy tắc nhân ta có 3.6.6 = 108
Vậy có 108 số cần tìm
Đúng 0
Bình luận (1)
Từ các số 1,2,3,4,5,6 có thể lập được bao nhiêu số tự nhiên,mỗi số có 6 chữ số đồng thời thỏa điều kiện :sáu số của mỗi số là khác nhau và trong mỗi số đó tổng của 3 chữ số đầu nhỏ hơn tổng của 3 số sau một đơn vị. A.104 B. 106 C.108 D.112
Đọc tiếp
Từ các số 1,2,3,4,5,6 có thể lập được bao nhiêu số tự nhiên,mỗi số có 6 chữ số đồng thời thỏa điều kiện :sáu số của mỗi số là khác nhau và trong mỗi số đó tổng của 3 chữ số đầu nhỏ hơn tổng của 3 số sau một đơn vị.
A.104
B. 106
C.108
D.112
Gọi ![]() là số cần lập a1 + a2 + a3 = 10
là số cần lập a1 + a2 + a3 = 10
Theo bài ra ta có: ![]() (1)
(1)
Mà ![]() và đôi một khác nhau nên
và đôi một khác nhau nên
a1,a2,a3,a4,a5,a6 = 1 + 2 + 3 + 4 + 5 + 6 =21
(2)
Từ (1), (2) suy ra: a1 + a2 + a3 = 10
Phương trình này có các bộ nghiệm là: ( a1 , a2 , a3 ) = (1,3,6); (1,4,5); (2,3,5)
Với mỗi bộ ta có 3!.3!=36 số.
Vậy có cả 3.36=108 số cần lập.
Chọn C.
Đúng 0
Bình luận (0)
Từ các số 1,2,3,4,5,6 có thể lập được bao nhiêu số tự nhiên, mỗi số có 6 chữ số đồng thời thỏa điều kiện. sáu số của mỗi số là khác nhau và trong mỗi số đó tổng của 3 chữ số đầu nhỏ hơn tổng của 3 số sau một đơn vị.
A. 104
B. 106
C. 108
D. 36
Từ các số 1,2,3,4,5,6 có thể lập được bao nhiêu số tự nhiên, mỗi số có 6 chữ số đồng thời thỏa điều kiện: sáu số của mỗi số là khác nhau và trong mỗi số đó tổng của 3 chữ số đầu nhỏ hơn tổng của 3 số sau một đơn vị. A. 104 B. 106 C. 108 D. 36
Đọc tiếp
Từ các số 1,2,3,4,5,6 có thể lập được bao nhiêu số tự nhiên, mỗi số có 6 chữ số đồng thời thỏa điều kiện: sáu số của mỗi số là khác nhau và trong mỗi số đó tổng của 3 chữ số đầu nhỏ hơn tổng của 3 số sau một đơn vị.
A. 104
B. 106
C. 108
D. 36
Chọn đáp án C
Cách 1: Gọi x = a 1 a 2 . . . a 6 ¯ , a i ∈ 1 , 2 , 3 , 4 , 5 , 6 là số cần lập
Theo bài ra ta có:
![]()
Mà a 1 , a 2 , a 3 , a 4 , a 5 , a 6 ∈ 1 , 2 , 3 , 4 , 5 , 6 và đôi một khác nhau nên
![]()
Từ (1), (2) suy ra: a 1 + a 2 + a 3 = 10
Phương trình này có các bộ nghiệm là:
![]()
Với mỗi bộ ta có 36 số.
Vậy có cả thảy 3.36=108 số cần lập.
Cách 2: Gọi x = a b c d e f là số cần lập
Ta có:
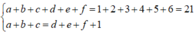
⇒ a + b + c = 11 .
Do a , b , c ∈ 1 , 2 , 3 , 4 , 5 , 6
Suy ra ta có các cặp sau:
![]()
Với mỗi bộ như vậy ta có 3! cách chọn a, b, c và 3! cách chọn d ,e ,f
Do đó: 3!.3!.3!= 108 số thỏa yêu cầu bài toán
Đúng 0
Bình luận (0)
Từ các số 1,2,3,4,5,6 có thể lập được bao nhiêu số tự nhiên, mỗi số có 6 chữ số đồng thời thỏa điều kiện. sáu số của mỗi số là khác nhau và trong mỗi số đó tổng của 3 chữ số đầu nhỏ hơn tổng của 3 số sau một đơn vị.
A. 104
B. 106
C. 108
D. 36