Biết z 1 và z 2 là hai nghiệm của phương trình 2 x 3 + 3 x + 3 = 0. Hãy tính: z 1 2 + z 2 2
PB
Những câu hỏi liên quan
Biết x; y; z khác 0 và (y +z + 1)/x = (x + z + 2)/y = (x + y - 3)/z=1/(x + y + z)
Khi đó (x + y + z)/2=....................
(điền kết quả là phân số tối giản)
Cái này là trong violympic! mk nhớ là 0.5 nhưng ko chắc chán hic!!!!!!!!!! TTT_TTT
Đúng 0
Bình luận (0)
Tìm x,y,z biết: x-1/2=y-2/3=z-3/4 và x-2y+3z= -10. Kết quả x,y,z là X=______;Y=______; Z=______?
Tìm số phức z biết |iz + 1 | = 2 và ( 1 + i) z + 1 – 2i là số thuần ảo.
A. z = 1
B. z = 1 + 2i
C. z = - 1 và z = 1+ 2i
D. Đáp án khác
Chọn C.
Đặt 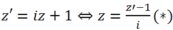 và
và ![]() khi đó ta có:
khi đó ta có:
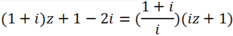
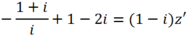
Số phức này là số ảo, do đó ta có: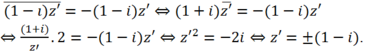
Thay vào (*) ta có z = -1 và z = 1+ 2i.
Đúng 0
Bình luận (0)
Cho x,y,z là số thực tùy ý biết x+y+z=0 và -1≤x≤1; -1≤y≤1; -1≤z≤1
Chứng minh x2+y4+z6≤2
1. Tìm x,y,z biết x+y+z= 1,5 và x^2 + y^2 + z^2 = 0,75
2. Cho a= (8^3)^100 - 1 là hợp số hay là số nguyên tố
Bài 1 : Tìm x ,y,z biết:
a, 3/x-1 = 4/y-2 = 5/z-3 và x+y+z = 18
b, 3/x-1 = 4/y-2 = 5/z-3 và x.y.z = 192
Bài 2 : Tìm x,y,z biết : x^3+y^3/6 = x^3-2y^3/4 và x^6.y^6 = 64
Bài 3 : Tìm x,y,z biết :x+4/6 = 3y-1/8 = 3y-x-5/x
Bài 4 :Tìm x,y,z biết : x+y+2005/z = y+z-2006 = z+x+1/y = 2/x+y+z
bài 1 : a,ta có 3/x-1 =4/y-2=5/z-3 => x-1/3=y-2/4=z-3/5
áp dụng .... => x-1+y-2+z-3 / 3+4+5 = x+y+z-1-2-3/3+4+5 = 12/12=1
do x-1/3 = 1 => x-1 = 3 => x= 4 ( tìm y,z tương tự
Đúng 2
Bình luận (0)
Bài 1:
a) Ta có: 3/x - 1 = 4/y - 2 = 5/z - 3 => x - 1/3 = y - 2/4 = z - 3/5 áp dụng ... =>x - 1 + y - 2 + z - 3/3 + 4 + 5 = x + y + z - 1 - 2 - 3/3 + 4 + 5 = 12/12 = 1 do x - 1/3 = 1 => x - 1 = 3 => x = 4 ( tìm y, z tương tự )
cũng dễ thôi
Xem thêm câu trả lời
1) Cho x, y, z là ba số dương phân biệt. Hãy tìm tỉ số x/y ,biết rằng:
y/x-z=x+y/z=x/y
2) Tìm các số x, y, z , biết rằng
x-1/2=y+3/4=z-5/6 và 5z-3x-4y=50
Biết rằng x,y và z là các số thực và thỏa mãn:\(\frac{x-1}{2}\)=\(\frac{y}{3}\)=\(\frac{z+2}{6}\). Biết rằng x+y+z=-5.Tính các giá trị của x,y và z
cho x,y,z là số nguyên biết 3x^2 = y(y+2) = (z-1)(z^2 +z + 1)
tìm x,y,z biết:
a, x/2=y/3 và y/5=z/7 và x+y+z=92
b, x/y+z+1=y/x+z+1=z/x+y-2=x+y+z
a) \(\frac{x}{2}=\frac{y}{3}\)và \(\frac{y}{5}=\frac{z}{7}\)và \(x+y+z=92\)
\(\Rightarrow\frac{x}{10}=\frac{y}{15}=\frac{z}{21}\)
Áp dụng tính chất dãy tỉ số = nhau
ta có
\(\frac{x}{10}=\frac{y}{15}=\frac{z}{21}=\frac{x+y+z}{10+15+21}=\frac{92}{46}=2\)
Suy ra \(\frac{x}{10}=2\Rightarrow x=2.10=20\)
\(\frac{y}{15}=2\Rightarrow y=2.15=30\)
\(\frac{z}{21}=2\Rightarrow z=2.21=42\)
Vậy \(x=20;y=30;z=42\)
Đúng 1
Bình luận (0)

