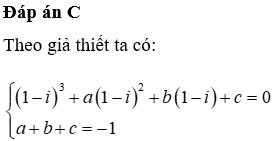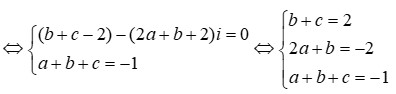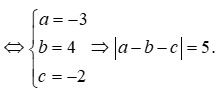Biết z 1 và z 2 là hai nghiệm của phương trình 2 x 3 + 3 x + 3 = 0. Hãy tính: z 1 z 2 + z 2 z 1
PB
Những câu hỏi liên quan
Cho hai số phức z_1,z_2z1,z2. Biết rằng z_1+z_2z1+z2 và z_1.z_2z1.z2 là hai số thực. Chứng tỏ rằng z_1,z_2z1,z2 là hai nghiệm của một phương trình bậc hai với hệ số thực ?
Cho phương trình
z
3
+
a
z
2
+
b
z
+
c
0
. Nếu
z
1
−
i
và
z
1
là hai nghiệm của phương trình thì
a
−
b
−
c
bằng (a, b, c là số thực). A. 2 B. 3 C. 5 D. 6
Đọc tiếp
Cho phương trình z 3 + a z 2 + b z + c = 0 . Nếu z = 1 − i và z = 1 là hai nghiệm của phương trình thì a − b − c bằng (a, b, c là số thực).
A. 2
B. 3
C. 5
D. 6
Bài 1: Biết x ; y ; z là nghiệm nguyên của phương trình x2 + y2 + z2 = xy + 3y + 2x - 4
Khi đó x + y + z = ?
Bài 2 : Số nghiệm nguyên dương của phương trình x2 - 2y2 = 5
Bài 3 : Phương trình x2 + y2 + 2x + 1 = 0 có nghiệm ( x;y) = (.......) ?
Giúp mk vs !!!
Bài 1:
\(x^2+y^2+z^2=xy+3y+2z-4\)
\(\Leftrightarrow4x^2+4y^2+4z^2=4xy+12y+8z-16\)
\(\Leftrightarrow4x^2+4y^2+4z^2-4xy-12y-8z+16=0\)
\(\Leftrightarrow\left(4x^2-4xy+y^2\right)+\left(3y^2-12y+12\right)+\left(4z^2-8z+4\right)=0\)
\(\Leftrightarrow\left(2x-y\right)^2+3\left(y-2\right)^2+4\left(z-1\right)^2=0\)
Xảy ra khi \(\left\{{}\begin{matrix}2x-y=0\\y-2=0\\z-1=0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x=z=1\\y=2\end{matrix}\right.\)
Khi đó \(x+y+z=1+1+2=4\)
Bài 2:
\(x^2-2y^2=5\)
Từ pt đầu ta có \(x\) phải là số lẻ. Thay \(x=2k+1\left(k\in Z\right)\) vào pt đầu ta được:
\(\left(2k+1\right)^2-2y^2=5\)
\(\Rightarrow4k^2+4k+1-2y^2=5\)
\(\Rightarrow4k^2+4k-4=2y^2\)
\(\Rightarrow4\left(k^2+k-1\right)=2y^2\)
\(\Rightarrow2\left(k^2+k-1\right)=y^2\). Đặt \(y=2t\left(t\in Z\right)\), ta có:
\(2\left(k^2+k-1\right)=4t^2\)
\(\Leftrightarrow k\left(k+1\right)=2t^2+1\)
Dễ thấy: \(VT\) là số chẵn \(\forall x\in Z\) còn \(VP\) là số lẻ \(\forall t\in Z\)
Suy ra pt vô nghiệm. Số nghiệm nguyên dương là \(0\)
Bài 3:
\(x^2+y^2+2x+1=0\)
\(\Leftrightarrow\left(x^2+2x+1\right)+y^2=0\)
\(\Leftrightarrow\left(x+1\right)^2+y^2=0\)
Xảy ra khi \(\left\{{}\begin{matrix}x+1=0\\y=0\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}x=-1\\y=0\end{matrix}\right.\)
Đúng 0
Bình luận (0)
1 . Ta có :
\(x^2+y^2+z^2=xy+3y+2z-4\)
\(\Leftrightarrow4x^2+4y^2+4z^2=4xy+12y+8z-16\)
\(\Leftrightarrow4x^2+4y^2+4z^2-4xy-12y-8z+16=0\)
\(\Leftrightarrow\left(4x^2-4xy+y^2\right)+3\left(y^2-4y+4\right)+4\left(z^2-2z+1\right)=0\)
\(\Leftrightarrow\left(2x-y\right)^2+3\left(y-2\right)^2+4\left(z-1\right)^2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x-y=0\\y-2=0\\z-1=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=z=1\\y=2\end{matrix}\right.\)
Vậy x+y+z = 1 + 2 + 1 = 4
Đúng 0
Bình luận (0)
2 . Ta có : \(x^2-2y^2=5\left(1\right)\)
Từ phương trình \(\left(1\right)\Rightarrow x\) phải là số lẻ .
Thay \(x=2k+1\left(k\in N\right)\) vào \(\left(1\right)\) , ta được :
\(4k^2+4k+1-2y^2=5\Leftrightarrow4k^2+4k-2y^2=4\)
\(\Leftrightarrow2k^2+2k-y^2=2\)
\(\Leftrightarrow2k^2+2k-2=y^2\)
\(\Leftrightarrow2\left(k^2+k-1\right)=y^2\)
\(\Rightarrow y^2\) là số chẵn \(\Rightarrow y\) là số chẵn .
Đặt y = 2t ( t \(\in Z\) ) , ta có :
\(2\left(k^2+k-1\right)=4t^2\Leftrightarrow k\left(k+1\right)=2t^2+1\left(\cdot\right)\)
* Nhận xét : \(k\left(k+1\right)\) là số chẵn ,
\(2t^2+1\) là số lẻ
\(\Rightarrow\) Phương trình \(\left(\cdot\right)\) vô nghiệm .
Vậy phương trình \(\left(1\right)\) không có nghiệm nguyên .
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Tìm số phức z là nghiệm chung của hai phương trình: iz + 1 = 0 và z 4 - 1 = 0
A. z = 1
B. z = -1
C. z = i
D. Không tồn tại
Chứng minh rằng hai số phức liên hợp z và z là hai nghiệm của một phương trình bậc hai với hệ số phức.
Nếu z = a + bi thì z + z = 2a ∈ R; z. z = a 2 + b 2 ∈ R
z và z là hai nghiệm của phương trình (x − z)(x − z ) = 0
⇔ x 2 − (z + z ) x + z. z = 0
⇔ x 2 − 2ax + a 2 + b 2 = 0
Đúng 0
Bình luận (0)
Chứng minh rằng hai số phức liên hợp z và z là hai nghiệm của một phương trình bậc hai với hệ số phức.
Nếu z = a + bi thì z + z = 2a ∈ R; z. z = a 2 + b 2 ∈ R
z và z là hai nghiệm của phương trình (x − z)(x − z ) = 0
⇔ x 2 − (z + z ) x + z. z = 0
⇔ x 2 − 2ax + a 2 + b 2 = 0
Đúng 0
Bình luận (0)
Cho phương trình
z
3
+
a
z
2
+
b
z
+
c
0
Nếu z1-i và z1 là 2 nghiệm của phương trình thì
a
-
b
-
c
bằng A. 2 B. 3 C. 5 D. 6
Đọc tiếp
Cho phương trình z 3 + a z 2 + b z + c = 0 Nếu z=1-i và z=1 là 2 nghiệm của phương trình thì a - b - c bằng
A. 2
B. 3
C. 5
D. 6
Gọi
z
1
và
z
2
là hai nghiệm phức của phương trình
z
2
+
z
+
1
0
. Tính giá trị của
z
1
2017
+...
Đọc tiếp
Gọi z 1 và z 2 là hai nghiệm phức của phương trình z 2 + z + 1 = 0 . Tính giá trị của z 1 2017 + z 2 2017
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Đáp án C
Phương pháp: Tính z 1 , z 2 và sử dụng công thức Moivre
Cách giải: Phương trình z 2 + z + 1 có ∆ = 1 - 4 = - 3 nên có 2 nghiệm
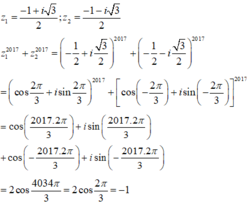
Đúng 0
Bình luận (0)
Gọi
z
1
và
z
2
là hai nghiệm phức của phương trình
z
2
+
z
+
1
0
. Tính giá trị của
z
1
2017
+
z
2
2017
A.
z
1
2017
+
z...
Đọc tiếp
Gọi z 1 và z 2 là hai nghiệm phức của phương trình z 2 + z + 1 = 0 . Tính giá trị của z 1 2017 + z 2 2017
A. z 1 2017 + z 2 2017 = 1
B. z 1 2017 + z 2 2017 = 2
C. z 1 2017 + z 2 2017 = -1
D. z 1 2017 + z 2 2017 = -2
Cho a, b, c ε R, a # 0, z1 và z2 là hai nghiệm của phương trình az2 + bz + c = 0
Hãy tính z1 + z2 và z1 z2 theo các hệ số a, b, c.