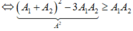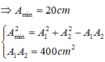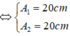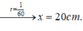Tổng hợp hai dao động x 1 = a 1 cos 10 t + π / 2 c m , x 2 = a 2 cos 10 t + 2 π / 3 c m ( a 1 , a 2 là các số thực) là dao động có phương trình x = 5 cos 10 t + π 6 c m . Chọn biểu thức đúng:
A. a 1 a 2 = - 2
B. a 1 . a 2 = - 50 3
C. a 1 . a 2 = 50 3
D. a 1 a 2 = 2