Trong mặt phẳng Oxy cho tam giác MNP với M 1 ; - 1 , N 3 ; 1 , P 5 ; - 5 ;. Tọa độ tâm I đường tròn ngoại tiếp tam giác MNP là:
A. I 4 ; 2
B. I - 4 ; 2
C. I 4 ; - 4
D. I 4 ; - 2
Trong mặt phẳng Oxy cho tam giác MNP với M 1 ; - 1 , N 3 ; 1 , P 5 ; - 5 ;. Tọa độ tâm I đường tròn ngoại tiếp tam giác MNP là:
A. I 4 ; 2
B. I - 4 ; 2
C. I 4 ; - 4
D. I 4 ; - 2
Trong mặt phẳng toạ độ Oxy, cho tam giác MNP vuông tại M. Biết điểm M(2,1); N(3,-2) và P là điểm nằm trên trục Ox. Tìm toạ độ điểm P và tính diện tích tam giác MNP
Do P thuộc Ox nên tọa độ có dạng \(P\left(p;0\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{MN}=\left(1;-3\right)\\\overrightarrow{MP}=\left(p-2;-1\right)\end{matrix}\right.\)
Do tam giác MNP vuông tại M \(\Rightarrow\overrightarrow{MN}.\overrightarrow{MP}=0\)
\(\Rightarrow1.\left(p-2\right)+3=0\) \(\Rightarrow p=-1\)
\(\Rightarrow P\left(-1;0\right)\)
\(\Rightarrow\overrightarrow{MP}=\left(-3;-1\right)\Rightarrow\left\{{}\begin{matrix}MN=\sqrt{1^2+\left(-3\right)^2}=\sqrt{10}\\MP=\sqrt{\left(-3\right)^2+\left(-1\right)^2}=\sqrt{10}\end{matrix}\right.\)
\(\Rightarrow S_{MNP}=\dfrac{1}{2}MN.MP=5\)
trong mặt phẳng tọa độ oxy biết M(2;3);N(6;2);P(5;0) tìm tọa độ trọng tâm G cửa tam giác MNp
Trong mặt phẳng tọa độ Oxy, cho ba điểm M, N, P là điểm biểu diễn của 3 số phức: z 1 = 8 + i ; z 2 = 1 + 4 i ; z 3 = 5 + x i .Tìm x để tam giác MNP vuông tại P
A. 1 và 2
B. 0 và 7
C. -1 và -7
D. 3 và 5
Ta có 3 điểm M ( 8;3 ), N ( 1;4 ), P ( 5;x ) ⇒ M P → - 3 ; x ; - 3 , N P → 4 ; x ; - 4
∆ M N P vuông tại P ⇔ M P → . N P → = 0 ⇔ - 12 + x - 3 x - 4 = 0 ⇔ x = 0 ; x = 7 .
Đáp án B
Trong mặt phẳng tọa độ Oxy, cho ba điểm M,N,P là điểm biểu diễn của 3 số phức: z 1 = 8 + 3 i ; z 2 = 1 + 4 i ; z 3 = 5 + x i .Với giá trị nào của x thì tam giác MNP vuông tại P?
A. 1 và 2
B. 0 và 7
C. -1 và -7
D. 3 và 5
Chọn B.
Ta có 3 điểm M(8;3), N(1;4), P(5;x)
![]()
Để ∆ MNP vuông tại P
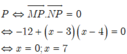
Trong mặt phẳng tọa độ Oxy, cho ba điểm M, N , P là điểm biểu diễn của 3 số phức: z 1 = 8 + 3 i , z 2 = 1 + 4 i , z 3 = 5 + x i .Với giá trị nào của x thì tam giác MNP vuông tại P?
A. 1 và 2
B. 0 và 7
C. - 1 và - 7
D. 3 và 5
Trong mặt phẳng tọa độ Oxy, cho ba điểm M, N , P là điểm biểu diễn của 3 số phức: z 1 = 8 + 3 i , z 2 = 1 + 4 i , z 3 = 5 + x i .Với giá trị nào của x thì tam giác MNP vuông tại P?
A. 1 và 2
B. 0 và 7
C. - 1 và - 7
D. 3 và 5
Trong mặt phẳng toạ độ Oxy, cho tam giác ABC có trung điểm các cạnh BC, CA, AB tương ứng là M(2 ; 0), N4 ; 2), P(1 ; 3).
a) Tìm toạ độ các điểm A, B, C.
b) Trọng tâm hai tam giác ABC và MNP có trùng nhau không? Vì sao?
a) Do M, N, P là trung điểm của các cạnh BC, CA, AB nên:
\(\left\{ \begin{array}{l}\frac{{{x_B} + {x_C}}}{2} = {x_M}\\\frac{{{x_B} + {x_A}}}{2} = {x_P}\\\frac{{{x_A} + {x_C}}}{2} = {x_N}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_B} + {x_C} = 4\\{x_B} + {x_A} = 2\\{x_A} + {x_C} = 8\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_A} = 3\\{x_B} = - 1\\{x_C} = 5\end{array} \right.\) và \(\left\{ \begin{array}{l}\frac{{{y_B} + {y_C}}}{2} = {y_M}\\\frac{{{y_B} + {y_A}}}{2} = {y_P}\\\frac{{{y_A} + {y_C}}}{2} = {y_N}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{y_B} + {y_C} = 0\\{y_B} + {y_A} = 4\\{y_A} + {y_C} = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{y_A} = 5\\{y_B} = - 1\\{y_C} = 1\end{array} \right.\)
Vậy \(A\left( {3;5} \right),B\left( { - 1; - 1} \right),C\left( {5;1} \right)\)
b) Trọng tâm tam giác ABC có tọa độ là: \(\left\{ \begin{array}{l}\frac{{{x_A} + {x_B} + {x_C}}}{3} = \frac{{3 + \left( { - 1} \right) + 5}}{3} = \frac{7}{3}\\\frac{{{y_A} + {y_B} + {y_C}}}{3} = \frac{{5 + \left( { - 1} \right) + 1}}{3} = \frac{5}{3}\end{array} \right.\)
Trọng tâm tam giác MNP có tọa độ là: \(\left\{ \begin{array}{l}\frac{{{x_M} + {x_N} + {x_P}}}{3} = \frac{{2 + 4 + 1}}{3} = \frac{7}{3}\\\frac{{{y_M} + {y_N} + {y_P}}}{3} = \frac{{0 + 2 + 3}}{3} = \frac{5}{3}\end{array} \right.\)
Vậy trọng tâm của 2 tam giác ABC và MNP là trùng nhau vì có cùng tọa độ.
Trong mặt phẳng Oxy, M,N,P là tọa độ điểm biểu diễn của số phức z 1 = - 5 + 6 i ; z 2 = - 4 - i ; z 3 = 4 + 3 i
Tọa độ trực tâm H của tam giác MNP là:
A. (3;1)
B. (-1;3)
C. (2;-3)
D. (-3;2)
Chọn D.
M(-5;6), N(-4;-1), P(4;3)
Gọi H(x;y) là trực tâm ∆ MNP, ta có:
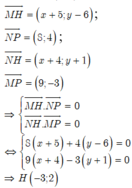
Trong mặt phẳng oxy M,N,P là tọa độ điểm biểu diễn của số phức z 1 = - 5 + 6 i , z 2 = - 4 - i ; z 3 = 4 + 3 i
Tọa độ trực tâm H của tam giác MNP là:
A. 3 ; 1
B. - 1 ; 3
C. 2 ; - 3
D. - 3 ; 2