Cho mặt phẳng (P) đi qua ba điểm A(0;1;0), B(-2;0;0), C(0;0;3). Phương trình của mặt phẳng (P) là:
A. P : 3 x + 6 y + 2 z = 6
B. P : 3 x - 6 y - 2 z + 6 = 0
C. P : - 3 x + 6 y + 2 z = 0
D. P : 6 x - 3 y + 2 z = 0
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A ( 3 ; 0 ; 0 ) , B ( 0 ; – 4 ; 0 ) , C ( 0 ; 0 ; 4 ) . Viết phương trình mặt phẳng (R) đi qua ba điểm A, B, C.
A. ( R ) : 4 x – 3 y + 3 z – 12 = 0
B. ( R ) : 4 x + 3 y + 3 z + 12 = 0
C. ( R ) : 3 x – 4 y + 4 z – 12 = 0
D. ( R ) : 3 x + 4 y + 4 z + 12 = 0 .
Đáp án là A
(R) là mặt phẳng có phương trình đoạn chắn là
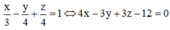
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(3;0;0), B(0;–4;0), C(0;0;4). Viết phương trình mặt phẳng (R) đi qua ba điểm A, B, C
A. (R) : 4x – 3y + 3z – 12 = 0
B. (R) : 4x + 3y + 3z + 12 = 0
B. (R) : 3x – 4y + 4z – 12 = 0
D. (R) : 3x + 4y + 4z + 12 = 0
Viết phương trình mặt phẳng: Đi qua ba điểm A(-3; 0; 0); B(0; -2; 0) và C(0; 0; -1).
Cách 1:
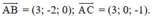
Mặt phẳng (R) đi qua ba điểm A, B, C nhận 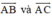 là hai vec tơ chỉ phương
là hai vec tơ chỉ phương
⇒ Nhận 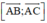 = ((-2).(-1) – 0; 0.3 – 3.(-1); 3.0 – 3.(-2)) = (2; 3; 6) là vec tơ pháp tuyến.
= ((-2).(-1) – 0; 0.3 – 3.(-1); 3.0 – 3.(-2)) = (2; 3; 6) là vec tơ pháp tuyến.
(R) đi qua A(-3; 0; 0) nên có phương trình:
2(x + 3) + 3y + 6z = 0
⇔ 2x + 3y + 6z + 6 = 0.
Cách 2 :
(R) đi qua A(-3 ; 0 ; 0) ; B(0 ; -2 ; 0) ; C(0 ; 0 ; -1) nên có phương trình đoạn chắn là :
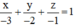
⇔ 2x + 3y + 6z + 6 = 0.
Viết phương trình mặt phẳng (P) đi qua ba điểm A(-3;0;0), B(0;-2;0), C(0;0;-1).
A. 2 x + 3 y + 6 z + 6 = 0
B. 2 x - 3 y + 6 z + 6 = 0
C. x 3 + y 2 + z 1 = 1
D. x 3 + y 2 + z 1 = 0
Cho ba điểm A(2;1;-1); B (-1;0;4); C (0; -2;-1) . Phương trình mặt phẳng đi qua A và vuông góc với BC là
![]()
![]()
![]()
![]()
Cho ba điểm A(2;1;-1); B (-1;0;4); C (0; -2;-1) . Phương trình mặt phẳng đi qua A và vuông góc với BC là
A. x - 2 y - 5 = 0
B. x - 2 y - 5 z + 5 = 0
C. 2 x - y + 5 z - 5 = 0
D. x - 2 y - 5 z - 5 = 0
Cho ba điểm A(3;1;1), B(0;1;4), C(-1;-3;1). Viết phương trình mặt cầu (S) đi qua A, B, C và có tâm nằm trên mặt phẳng (P): x+y-2z+4=0
![]()
![]()
![]()
![]()
Cho ba điểm A(3;1;1), B(0;1;4), C(-1;-3;1). Viết phương trình mặt cầu (S) đi qua A, B, C và có tâm nằm trên mặt phẳng (P):x+y-2z+4=0
A. x + 1 2 + y - 1 2 + z + 2 2 = 9
B. x - 1 2 + y + 1 2 + z - 2 2 = 3
C. x - 1 2 + y + 1 2 + z - 2 2 = 9
D. x + 1 2 + y - 1 2 + z + 2 2 = 3
Chọn C
Gọi tâm mặt cầu I(x;-x+2z-4;z). Tìm x,z từ hệ hai phương trình IA=IB=IC
Trong không gian có hệ tọa độ Oxyz, cho ba điểm A(0;1;2), B(0;-2;0), C(-1;0;1). Mặt phẳng (P) đi qua A, trực tâm H của tam giác ABC và vuông góc với mặt phẳng (ABC) có phương trình là
A. 4x + 2y - z + 4 = 0
B. 4x + 2y + z - 4 = 0
C. 4x - 2y - z + 4 = 0
D. 4x - 2y + z + 4 = 0