Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Các câu hỏi tương tự
Trong không gian với hệ toạ độ Oxyz, cho ba điểm A(2;-1;1), B(1;0;4) và C(0;-2;-1). Phương trình mặt phẳng qua A và vuông góc với đường thẳng BC là: A. 2x + y + 2z - 5 0 B. x + 2y + 5z + 5 0 C. x - 2y + 3z - 7 0 D. x + 2y + 5z - 5 0
Đọc tiếp
Trong không gian với hệ toạ độ Oxyz, cho ba điểm A(2;-1;1), B(1;0;4) và C(0;-2;-1). Phương trình mặt phẳng qua A và vuông góc với đường thẳng BC là:
A. 2x + y + 2z - 5 =0
B. x + 2y + 5z + 5 =0
C. x - 2y + 3z - 7 =0
D. x + 2y + 5z - 5 =0
Trong không gian Oxyz, cho ba điểm A(4;3;2), B(-1;-2;1) và C(-2;2;-1). Phương trình mặt phẳng đi qua A và vuông góc với BC là: A. x - 4y + 2z + 4 0 B. x - 4y - 2z + 4 0 C. x - 4y - 2z - 4 0 D. x + 4y - 2z - 4 0.
Đọc tiếp
Trong không gian Oxyz, cho ba điểm A(4;3;2), B(-1;-2;1) và C(-2;2;-1). Phương trình mặt phẳng đi qua A và vuông góc với BC là:
A. x - 4y + 2z + 4 = 0
B. x - 4y - 2z + 4 = 0
C. x - 4y - 2z - 4 = 0
D. x + 4y - 2z - 4 = 0.
Trong không gian với hệ trục tọa độ Oxyz, cho các điểm A(0;1;2), B(2;-2;1), C(-2;0;1). Phương trình mặt phẳng đi qua A và vuông góc với BC là:
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho các điểm A(0;1;2), B(2;-2;1), C(-2;0;1). Phương trình mặt phẳng đi qua A và vuông góc với BC là:
![]()
![]()
![]()
![]()
Trong không gian với hệ toạ độ Oxyz, cho ba điểm A(2; -1; 1),B(1; 0;4) và C(0; -2; -1). Phương trình mặt phẳng qua A và vuông góc với đường thẳng BC là: A. 2x+y+2z-50 B. x+2y+5z+50 C. x-2y+3z-70 D. x+2y+5z-50.
Đọc tiếp
Trong không gian với hệ toạ độ Oxyz, cho ba điểm A(2; -1; 1),B(1; 0;4) và C(0; -2; -1). Phương trình mặt phẳng qua A và vuông góc với đường thẳng BC là:
A. 2x+y+2z-5=0
B. x+2y+5z+5=0
C. x-2y+3z-7=0
D. x+2y+5z-5=0.
Trong không gian với hệ toạ độ Oxyz, cho mặt phẳng
P
:
2
x
-
y
+
z
+
3
0
và điểm A(1;-2;1). Phương trình đường thẳng đi qua A và vuông góc với (P) là:
Đọc tiếp
Trong không gian với hệ toạ độ Oxyz, cho mặt phẳng P : 2 x - y + z + 3 = 0 và điểm A(1;-2;1). Phương trình đường thẳng đi qua A và vuông góc với (P) là:
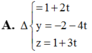
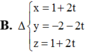
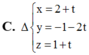
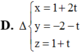
Trong không gian Oxyz, phương trình mặt phẳng (P) đi qua điểm B(2;1;-3), đồng thời vuông góc với hai mặt phẳng
Q
:
x
+
y
+
3
z
0
và
R
:
2
x
-
y
+
z
0
là:
Đọc tiếp
Trong không gian Oxyz, phương trình mặt phẳng (P) đi qua điểm B(2;1;-3), đồng thời vuông góc với hai mặt phẳng Q : x + y + 3 z = 0 và R : 2 x - y + z = 0 là:
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có
A
(
2
;
1
;
-
2
)
;
B
(
4
;
-
1
;
1
)
v
à
C
(
0
;
-
3
;
1
)
.
Phương trình d đi qua trọng tâm của tam giác ABC và vuông góc v...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có A ( 2 ; 1 ; - 2 ) ; B ( 4 ; - 1 ; 1 ) v à C ( 0 ; - 3 ; 1 ) . Phương trình d đi qua trọng tâm của tam giác ABC và vuông góc với mặt phẳng (ABC) là
A. x = 2 + t y = - 1 - 2 t z = - 2 t
B. x = - 2 + t y = - 1 - 2 t z = - 2 t
C. x = 2 + t y = 1 - 2 t z = - 2 t
D. x = 2 + t y = 1 + 2 t z = 2 t
Trong không gian với hệ tọa độ Oxyz cho điểm A(1;1;0) , B(2;-2;1) và (P): 4x + y + z - 3 0. Lập phương trình mặt phẳng (Q) đi qua A, B và tạo với mặt phẳng (P) một góc
60
o
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz cho điểm A(1;1;0) , B(2;-2;1) và (P): 4x + y + z - 3 = 0. Lập phương trình mặt phẳng (Q) đi qua A, B và tạo với mặt phẳng (P) một góc 60 o
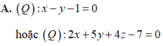
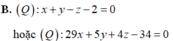
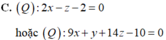
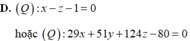
Trong không gian Oxyz, cho hai điểm A(1 ;0 ;-2), B(-1 ;1 ;2). Phương trình của mặt phẳng (P) đi qua A và vuông góc với đường thẳng AB là: A. 2x - y - 4z - 10 0 B. 2x - y - 4z + 10 0 C. x - y - 2z - 5 0 D. 2x - y - 3z + 8 0
Đọc tiếp
Trong không gian Oxyz, cho hai điểm A(1 ;0 ;-2), B(-1 ;1 ;2). Phương trình của mặt phẳng (P) đi qua A và vuông góc với đường thẳng AB là:
A. 2x - y - 4z - 10 = 0
B. 2x - y - 4z + 10 = 0
C. x - y - 2z - 5 = 0
D. 2x - y - 3z + 8 = 0



