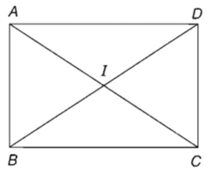
Cho hình chữ nhật ABCD có tâm I và cạnh AB = 1, AD = √3. Tính số đo các góc ∠(AID) và ∠(DIC) .
PB
Những câu hỏi liên quan
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Cạnh SA vuông góc với đáy ABa, ADa
2
, SAa
3
. Số đo của góc giữa SC và mặt phẳng (ABCD) bằng A. 300 B. 450 C. 600 D. 750
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Cạnh SA vuông góc với đáy AB=a, AD=a 2 , SA=a 3 . Số đo của góc giữa SC và mặt phẳng (ABCD) bằng
A. 300
B. 450
C. 600
D. 750
Đáp án là B
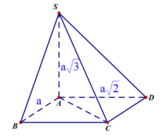
Vì SA vuông góc với đáy nên góc φ giữa SC và mặt phẳng (ABCD) bằng góc giữa SC và hình chiếu AC của nó lên đáy. Suy ra φ = S C A ^ (vì S C A ^ là góc nhọn trong tam giác vuông SAC)
Trong hình chữ nhật ABCD, ta có AC=a 3 . Suy ra tam giác SAC vuông cân ở A.
Vậy, số đo của góc giữa SC và mặt phẳng (ABCD) bằng 450
Đúng 0
Bình luận (0)
Cho hình chóp Sabcd có sa vuông góc với abcd , đáy abcd là hình chữ nhật có cạnh ab=a, ad=2a , sa= 2a căn 3
Gọi I là trung điểm của ab , mặt phẳng P qua I và vuông góc với Sb . Tính góc giữa mặt phẳng Sb và mp abcd
Giups mìnhhh với các bạn ơii , mk cần lời giải chi tiết , cảm ơnn nhiềuuu ah
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, ABa; AD2a, cạnh bên SA vuông góc với đáy và thể tích khối chóp S.ABCD bằng
2
a
3
3
. Tính số đo góc giữa đường thẳng SB với mặt phẳng (ABCD). A.
30
0
B.
60
0
C.
45
0
D. ...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB=a; AD=2a, cạnh bên SA vuông góc với đáy và thể tích khối chóp S.ABCD bằng 2 a 3 3 . Tính số đo góc giữa đường thẳng SB với mặt phẳng (ABCD).
A. 30 0
B. 60 0
C. 45 0
D. 75 0
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật,
A
B
a
;
A
D
2
a
, cạnh bên SA vuông góc với đáy và thể tích khối chóp S.ABCD bằng
2
a
3
3
. Tính số đo góc giữa đường thẳng SB với mặt phẳng (ABCD). A.
30
°
B.
60
°
C....
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, A B = a ; A D = 2 a , cạnh bên SA vuông góc với đáy và thể tích khối chóp S.ABCD bằng 2 a 3 3 . Tính số đo góc giữa đường thẳng SB với mặt phẳng (ABCD).
A. 30 °
B. 60 °
C. 45 °
D. 75 °
Đáp án C
Phương pháp: Thể tích khối chóp V = 1 3 S d . h : h là chiều cao của khối chóp, S là diện tích đáy.
Phương pháp xác định góc giữa đường thẳng và mặt phẳng: Góc giữa đường thẳng và mặt phẳng chính là góc giữa đường thẳng đó và hình chiếu của nó trên mặt phẳng.
Đúng 0
Bình luận (0)
Cho hình chóp SABCD có đáy ABCD là hình chữ nhật, AB1, AD2 cạnh bên SA vuông góc với đáy và
S
A
5
α
là số đo góc giữa hai mặt phẳng (SAB) và (SBD), cosα A.
145
29
B.
5
5
C.
6
6
D.
29
25
Đọc tiếp
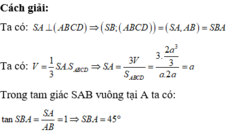
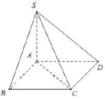
Cho hình chóp SABCD có đáy ABCD là hình chữ nhật, AB=1, AD=2 cạnh bên SA vuông góc với đáy và S A = 5 α là số đo góc giữa hai mặt phẳng (SAB) và (SBD), cosα
A. 145 29
B. 5 5
C. 6 6
D. 29 25
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB1, AD2 cạnh bên SA vuông góc với đáy và
S
A
5
.
α
là số đo góc giữa hai mặt phẳng (SAB) và (SBD),
cos
α
?
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB=1, AD=2 cạnh bên SA vuông góc với đáy và S A = 5 . α là số đo góc giữa hai mặt phẳng (SAB) và (SBD), cos α = ?
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Cạnh SA vuông góc với đáy
A
B
a
,
A
D
a
2
,
S
A
a
3
. Số đo của góc giữa SC và mặt phẳng (ABCD) bằng A.
60
0
B.
45
0
C.
30
0...
Đọc tiếp
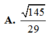
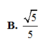
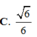
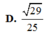
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Cạnh SA vuông góc với đáy A B = a , A D = a 2 , S A = a 3 . Số đo của góc giữa SC và mặt phẳng (ABCD) bằng
A. 60 0
B. 45 0
C. 30 0
D. 75 0
Đáp án A
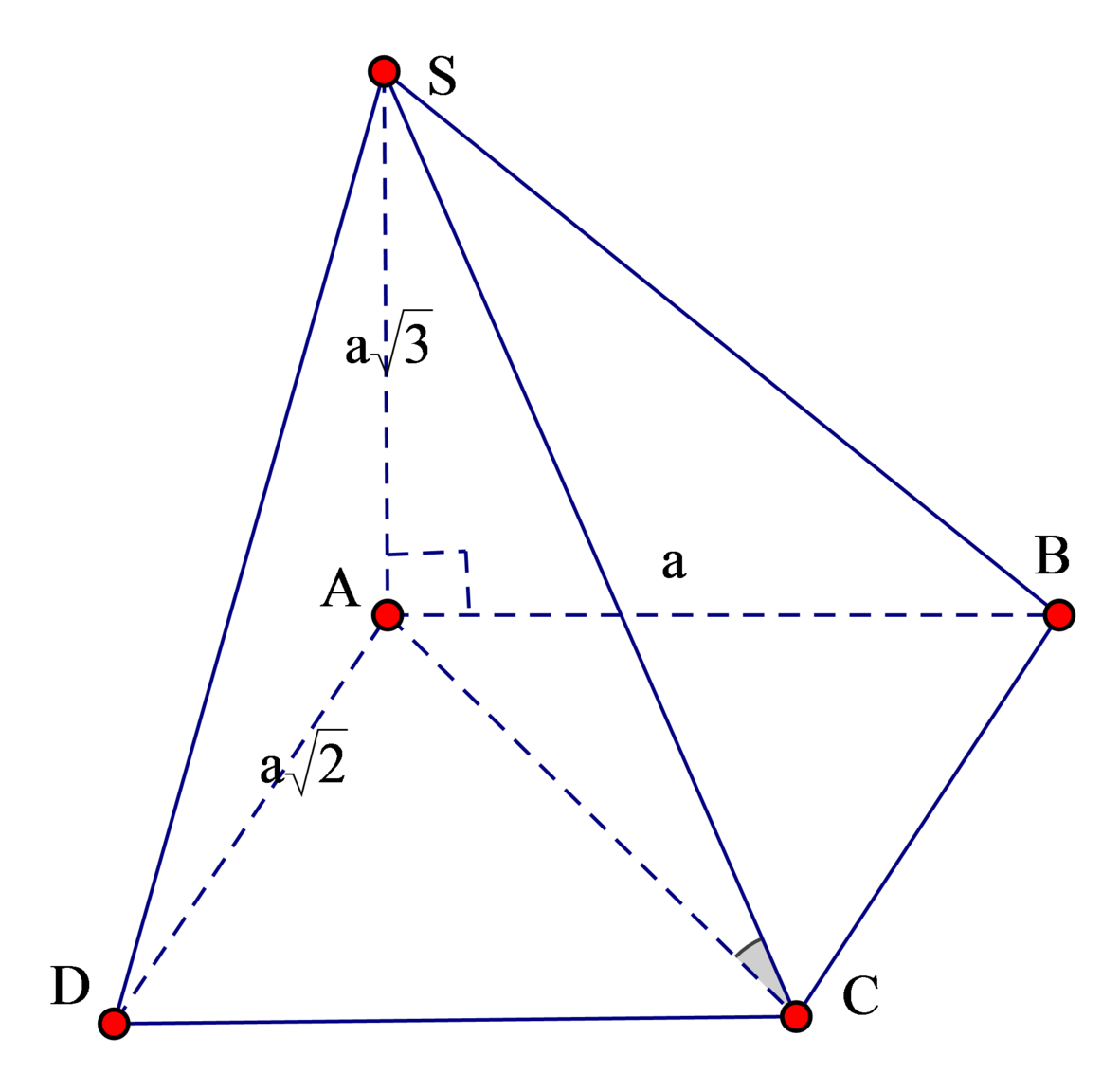
Góc giữa mặt phẳng và đường thẳng là góc tạo bởi đường thẳng đó với hình chiếu của nó lên mặt phẳng. Ở đây S A ⊥ A B C D ⇒ góc S C A = α là góc giữa Sc và (ABCD)
Ta có:
Tan α = S A A C = S A A B 2 + A D 2 = 3 a a 2 + 2 a 2 = 3
⇒ α = 60 0
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Cạnh SA vuông góc với đáy ABa,
A
D
a
2
,
S
A
a
3
. Số đo của góc giữa SC và mặt phẳng (ABCD) bằng A.
30
0
B.
45
0
C.
60
0
D.
75...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Cạnh SA vuông góc với đáy AB=a, A D = a 2 , S A = a 3 . Số đo của góc giữa SC và mặt phẳng (ABCD) bằng
A. 30 0
B. 45 0
C. 60 0
D. 75 0
Cho hình chữ nhật ABCD (Hình 1)
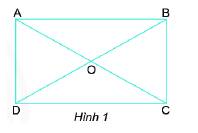
a) Đo rồi so sánh các cạnh và góc của hình chữ nhật.
b) Hãy kiểm tra xem hai cặp cạnh AB và CD, BC và AD có song song với nhau không?
c) AC và BD được gọi là hai đường chéo của hình chữ nhật.
Hãy đo rồi so sánh AC và BD.
a) Các cạnh đối diện của hình chữ nhật bằng nhau (AB = CD = 4,5 cm, BC = AD = 2,5 cm).
Các góc của hình chữ nhật đều bằng nhau và bằng \( 90^0\)
b) AB và CD song song với nhau.
AD và BC song song với nhau.
c) AC và BD bằng nhau (cùng bằng 5,1 cm).
Đúng 0
Bình luận (0)