Hẳn là nhiều người trong chúng ta mất nhiều năm trời học qua cấp 1, cấp 2 và cấp 3 để thoát khỏi môn Toán (để rồi lên Đại học lại dính phải Toán Cao Cấp như tôi chả hạn). Các bạn nghĩ bài tập toán giao về nhà sau mỗi tiết học là khoai ư? Vậy thì các bạn hãy nhìn vào bài toán này đây, để giải nó cần tới 3 nhà toán học và 200 terabyte dung lượng chỉ để chứa lời giải, đấy là đã có một siêu máy tính giúp sức rồi đấy nhé!Bạn cứ tính, 1 terabyte chứa được 337.920 bản Chiến Tranh Và Hòa Bình, bộ tiểu t...
Đọc tiếp
Hẳn là nhiều người trong chúng ta mất nhiều năm trời học qua cấp 1, cấp 2 và cấp 3 để thoát khỏi môn Toán (để rồi lên Đại học lại dính phải Toán Cao Cấp như tôi chả hạn). Các bạn nghĩ bài tập toán giao về nhà sau mỗi tiết học là khoai ư? Vậy thì các bạn hãy nhìn vào bài toán này đây, để giải nó cần tới 3 nhà toán học và 200 terabyte dung lượng chỉ để chứa lời giải, đấy là đã có một siêu máy tính giúp sức rồi đấy nhé!
Bạn cứ tính, 1 terabyte chứa được 337.920 bản Chiến Tranh Và Hòa Bình, bộ tiểu thuyết của Lev Tolstoy, bộ tiểu thuyết dài nhất trong lịch sử loài người, vậy thì 200 terabyte sẽ chứa lượng chữ nhiều khủng khiếp đến nhường nào.
Bài toán này khó đến mức nào mà bài giải lại vĩ đại tới vậy? Đó là một vấn đề toán học xoay quanh định lý Pythagoras (hay chúng ta vẫn biết nó dưới tên định lý Py-ta-go), được đưa ra lần đầu tiên bởi giáo sư toán học Ronald Graham hồi những năm 1980. Có tên là Biến Số Đúng Sai Của Bộ Ba Số Nguyên Dương Pythagoras (Boolean Pythagorean Triples), vấn đề toán học này “khoai” đến mức Graham đã treo giải 100 USD cho bất kì ai giải được (năm 1980 nhé!).
Vấn đề toán học này xoay quanh công thức của định lý Pythagoras: a^2 b^2 = c^2. Trong đó a và b là hai cạnh góc vuông của một tam giác vuông, còn c là cạnh huyền.

Công thức của định lý Pythagoras.
Giải thích về tên của vấn đề toán học này:
Bolean là biến có giá trị đúng hoặc sai.
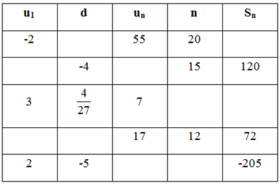


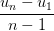 , Sn =
, Sn = 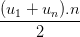
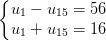
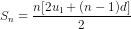
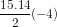 .
.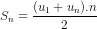 . Đáp số: n = 28, Sn = 140.
. Đáp số: n = 28, Sn = 140.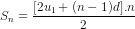 , từ đây tìm được n, tiếp theo áp dụng công thức un = u1 + (n - 1)d. Đáp số: n = 10, un = -43
, từ đây tìm được n, tiếp theo áp dụng công thức un = u1 + (n - 1)d. Đáp số: n = 10, un = -43



