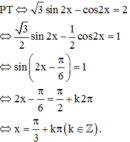Giải phương trình sau: 2sin2 x + sinx.cosx – 3cos2 x = 0
PB
Những câu hỏi liên quan
giải các phương trình sau : a). sin 2x+sin2 x=1/2
b.2sin2 x +3 sin x cosx + cos2 x= 0
c.sin2 x/2 + sin x - 2 cos 2 x/2 = 1/2
Giải phương trình 3cos2 6x + 8sin3x cos3x – 4 = 0.
3cos2 6x + 8sin3x cos3x - 4 = 0
⇔3(1-sin26x)+ 4sin6x - 4 = 0
⇔-3sin26x + 4sin6x - 1 = 0
Đặt sin6x = t với điều kiện -1 ≤ t ≤ 1 (*),
ta được phương trình bậc hai theo t:
-3t2 + 4t - 1 = 0(1)
Δ = 42 - 4.(-1).(-3) = 4
Phương trình (1)có hai nghiệm là:
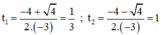 (thỏa mãn (*)
(thỏa mãn (*)
Ta có:
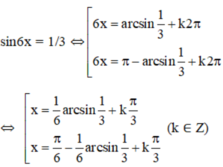
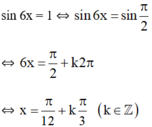
Đúng 0
Bình luận (0)
Giải phương trình
2
sin
2
x
+
3
sin
2
x
3
Đọc tiếp
Giải phương trình 2 sin 2 x + 3 sin 2 x = 3
![]()
![]()
![]()
![]()
Giải phương trình 4cos^3 x - 4cosx -sinx.cosx+1=0
Giải phương trình sau: 3sin2 x – 4 sinx.cosx + 5 cos2 x =2
3sin2x – 4sinx.cosx + 5cos2x = 2
⇔ 3sin2x – 4sinx.cosx + 5cos2x = 2(sin2x + cos2x)
⇔ sin2x – 4sinx.cosx + 3 cos2x = 0 (1)
+ Xét cosx = 0 ⇒ sin2x = 1.
Phương trình (1) trở thành 1 = 0 (Vô lý).
+ Xét cos x ≠ 0. Chia hai vế phương trình cho cos2x ta được
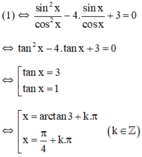
Vậy phương trình có tập nghiệm
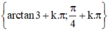 (k ∈ Z)
(k ∈ Z)
Đúng 0
Bình luận (0)
Nghiệm của phương trình 2sin2 x- 3sin x+ 1 0 thỏa điều kiện:
0
≤
x
π
2
A. x
π
/6 B. x
π
/4 C. x
π
/2 D. x -
π
/2
Đọc tiếp
Nghiệm của phương trình 2sin2 x- 3sin x+ 1= 0 thỏa điều kiện: 0 ≤ x < π 2
A. x = π /6
B. x = π /4
C. x = π /2
D. x = - π /2

Vì 0 ≤ x < π 2 nên nghiệm của phương trình là x = π /6
Đúng 0
Bình luận (0)
Nghiệm của phương trình 3cos2 x - 8cosx - 5 là:
Đọc tiếp
Nghiệm của phương trình 3cos2 x = - 8cosx - 5 là:
![]()
![]()
![]()
![]()
Giải các phương trình sau:
\(\begin{array}{l}a)\;sin2x + cos3x = 0\\b)\;sinx.cosx = \frac{{\sqrt 2 }}{4}\\c)\;sinx + sin2x = 0\end{array}\)
\(\begin{array}{l}a)\;sin2x + cos3x = 0\\ \Leftrightarrow cos\left( {\frac{\pi }{2} - 2x} \right) + cos3x = 0\\ \Leftrightarrow cos\left( {\frac{\pi }{2} - 2x} \right) = - cos3x\\ \Leftrightarrow cos\left( {\frac{\pi }{2} - 2x} \right) = cos\left( {\pi - 3x} \right)\\ \Leftrightarrow \left[ \begin{array}{l}\frac{\pi }{2} - 2x = \pi - 3x + k2\pi \\\frac{\pi }{2} - 2x = - \pi + 3x + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{2} + k2\pi \\x = \frac{{3\pi }}{{10}} + k\frac{{2\pi }}{5}\end{array} \right.\left( {k \in \mathbb{Z}} \right)\end{array}\)
\(\begin{array}{l}b)\;sinx.cosx = \frac{{\sqrt 2 }}{4}\\ \Leftrightarrow \frac{1}{2}\;sin2x = \frac{{\sqrt 2 }}{4}\\ \Leftrightarrow sin2x = \frac{{\sqrt 2 }}{2} = sin\left( {\frac{\pi }{4}} \right)\\ \Leftrightarrow \left[ \begin{array}{l}2x = \frac{\pi }{4} + k2\pi \\2x = \pi - \frac{\pi }{4} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{8} + k\pi \\x = \frac{{3\pi }}{8} + k\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\end{array}\)
\(\begin{array}{l}c)\;sinx + sin2x = 0\\ \Leftrightarrow sinx = - sin2x\\ \Leftrightarrow sinx = sin( - 2x)\\ \Leftrightarrow \left[ \begin{array}{l}x = - 2x + k2\pi \\x = \pi + 2x + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = k\frac{{2\pi }}{3}\\x = - \pi + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\end{array}\)
Đúng 0
Bình luận (0)
Giải pt lg sau : 3sin²x - 2√3.sinx.cosx - 3cos²x = 0.
Pt: \(\Rightarrow-3\left(cos^2x-sin^2x\right)-\sqrt{3}sin2x=0\)
\(\Rightarrow-3cos2x-\sqrt{3}sin2x=0\)
\(\Rightarrow sin2x+\sqrt{3}cos2x=0\)
\(\Rightarrow2sin\left(2x+\dfrac{\pi}{3}\right)=0\) \(\Rightarrow sin\left(2x+\dfrac{\pi}{3}\right)=0\)
\(\Rightarrow2x+\dfrac{\pi}{3}=k\pi\left(k\in Z\right)\)
\(\Rightarrow x=-\dfrac{\pi}{6}+k\dfrac{\pi}{2}\)
Đúng 1
Bình luận (0)