Giá trị lớn nhất của hàm số y = cos 2 x + 2 cosx + 1 là
A. 5
B. 2
C. 0
D. 4
PB
Những câu hỏi liên quan
Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau:1,y5-3cosx2,y3cos^2x-2cosx+23,ycos^2x+2cos2x4,ysqrt{5-2sin^2x.cos^2x}5,ycos2x-cosleft(2x-dfrac{pi}{3}right)6,ysqrt{3}sinx-cosx-27,y2cos^2x-sin2x+58,y2sin^2x-sin2x+109,ysin^6x+cos^6x
Đọc tiếp
Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau:
1,\(y=5-3cosx\)
2,\(y=3cos^2x-2cosx+2\)
3,\(y=cos^2x+2cos2x\)
4,\(y=\sqrt{5-2sin^2x.cos^2x}\)
5,\(y=cos2x-cos\left(2x-\dfrac{\pi}{3}\right)\)
6,\(y=\sqrt{3}sinx-cosx-2\)
7,\(y=2cos^2x-sin2x+5\)
8,\(y=2sin^2x-sin2x+10\)
9,\(y=sin^6x+cos^6x\)
Giá trị nhỏ nhất của hàm số sau trên khoảng (0;
π
/2) là:
y
1
sinx
+
cosx
A. 1 B. 2
2
C. -
2
D.
2
/2
Đọc tiếp
Giá trị nhỏ nhất của hàm số sau trên khoảng (0; π /2) là:
y = 1 sinx + cosx
A. 1 B. 2 2
C. - 2 D. 2 /2
Đáp án: D.
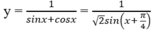
Trên khoảng (0; π /2), sin(x + π /4) ≤ 1;
Dấu "=" xảy ra ⇔ x = π /4
Suy ra giá trị nhỏ nhất của hàm số là min y = y( π /4) = 2 /2.
Đúng 0
Bình luận (0)
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số
a) \(y=f\left(x\right)=\dfrac{4}{\sqrt{5-2\cos^2x\sin^2x}}\)
b)\(y=f\left(x\right)=3\sin^2x+5\cos^2x-4\cos2x-2\)
c)\(y=f\left(x\right)=\sin^6x+\cos^6x+2\forall x\in\left[\dfrac{-\pi}{2};\dfrac{\pi}{2}\right]\)
Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số y = cos x + cos x - π 3
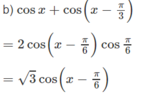
Vậy giá trị nhỏ nhất của y là -√3 đạt được chẳng hạn, tại x = 7π/6; giá trị lớn nhất của y là √3, đạt được chẳng hạn tại x = π/6
Đúng 0
Bình luận (0)
Bài 1: Tìm giá trị lớn nhất, nhỏ nhất của hàm số
y = \(cos^4x-sin^4x+3\)
Bài 2: Gỉai các phương trình lượng giác sau
a) \(3-cosx+6sinx-sin2x=0\)
b) \(sin^4x+cos^4x=\frac{1}{2}\)
c) \(1+cosx+cos3x=-cos2x\)
Tìm giá trị lớn nhất của hàm số
y
x
+
2
.
cos
x
trên
0
,
π
2
A
.
2
B...
Đọc tiếp
Tìm giá trị lớn nhất của hàm số y = x + 2 . cos x trên 0 , π 2
A . 2
B . 3
C . π 4 + 1
D . π 2
1/ tìm TXĐ chủa hàm số y = căn 1 - cosx /2 + sinx.
2/ tìm tập giá trị của hàm số y = 2-cos2x.
3/ Tìm giá trị lớn nhất và nhỏ nhất của các hàm số sau :
a) y=1 + 2sinx b)y=1 - 2cos^2x
4/ Tìm giá trị nhỏ nhất của hàm số y=tan^2x - 2tanx +3.
1. Không dịch được đề
2.
\(-1\le cos2x\le1\Rightarrow1\le y\le3\)
3.
a. \(-2\le2sinx\le2\Rightarrow-1\le y\le3\)
\(y_{min}=-1\) khi \(sinx=-1\Rightarrow x=-\dfrac{\pi}{2}+k2\pi\)
\(y_{max}=3\) khi \(sinx=1\Rightarrow x=\dfrac{\pi}{2}+k2\pi\)
b.
\(0\le cos^2x\le1\Rightarrow-1\le y\le2\)
\(y_{min}=-1\) khi \(cos^2x=1\Rightarrow x=k\pi\)
\(y_{max}=2\) khi \(cosx=0\Rightarrow x=\dfrac{\pi}{2}+k\pi\)
4.
\(y=\left(tanx-1\right)^2+2\ge2\)
\(y_{min}=2\) khi \(tanx=1\Rightarrow x=\dfrac{\pi}{4}+k\pi\)
Đúng 0
Bình luận (0)
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số
a) y=f(x)=\(\dfrac{4}{\sqrt{5-2cos^2xsin^2x}}\)
b)y=f(x)=\(3sin^2x+5cos^2x-4cos2x-2\)
c)y=f(x)=\(sin^6x+cos^6x+2\forall x\in\left[\dfrac{-\pi}{2};\dfrac{\pi}{2}\right]\)
Câu 1 : Giá trị lớn nhất của biểu thức P= 3 sin x +4 cosx là
Câu 2: Tính giá trị của biểu thức P=(sin²x-1)tan²x+ (cos²x-1)cot²x
Câu 3: Tìm các giá trị của tham số m để phương trình (x-2)(x-2mx+1)=0 có 2 nghiệm phân biệt
Xem chi tiết
Bài 2 : Tìm giá trị lớn nhất , giá trị nhỏ nhất của hàm số sau
a , y = 2sin3x+1
b, y = 1+cos22x
c , y = sinx+cosx+2
d , y = 3cosx -cos 2x +5
a/ \(-1\le sin3x\le1\Rightarrow-1\le y\le3\)
\(y_{min}=-1\) khi \(sin3x=-1\)
\(y_{max}=3\) khi \(sin3x=1\)
b/ \(0\le cos^22x\le1\Rightarrow1\le y\le2\)
\(y_{min}=1\) khi \(cos^22x=0\)
\(y_{max}=3\) khi \(cos^22x=1\)
c/ \(y=\sqrt{2}sin\left(x+\frac{\pi}{4}\right)+2\Rightarrow-\sqrt{2}+2\le y\le\sqrt{2}+2\)
\(y_{min}=-\sqrt{2}+2\) khi \(sin\left(x+\frac{\pi}{4}\right)=-1\)
\(y_{max}=\sqrt{2}+2\) khi \(sin\left(x+\frac{\pi}{4}\right)=1\)
d/ \(y=3cosx-\left(2cos^2x-1\right)+5=-2cos^2x+3cosx+6\)
\(y=-2\left(cosx-\frac{3}{4}\right)^2+\frac{57}{8}\le\frac{57}{8}\)
\(y_{max}=\frac{57}{8}\) khi \(cosx=\frac{3}{4}\)
\(y=\left(cosx+1\right)\left(-2cosx+5\right)+1\ge1\)
\(y_{min}=1\) khi \(cosx=-1\)