Trong hệ tọa độ Oxy, cho ba điểm A(1; 3); B(-1; 2); C(-2; 1). Tìm tọa độ của vectơ A B → − A C → .
A. (-5; -3)
B. (1; 1)
C. (-1; 2)
D. (-1; 1)
. Trong hệ tọa độ , Oxy cho ba điểm A(1;3),B(-1;2),C(-2;1). Tìm tọa độ của vectơ AB - AC
giải chi tiết nha
\(\left\{{}\begin{matrix}\overrightarrow{AB}=\left(-2;-1\right)\\\overrightarrow{AC}=\left(-3;-2\right)\end{matrix}\right.\)
\(\Rightarrow\overrightarrow{AB}-\overrightarrow{AC}=\left(-2-\left(-3\right);-1-\left(-2\right)\right)=\left(1;1\right)\)
Trong cùng hệ trục tọa độ Oxy cho ba điểm A(2;4), B(-3;-1), C(-2;1). Chứng minh ba điểm A,B,C không thẳng hàng
Ta có:
vt AB(Xb-Xa;Yb-Ya)=(-3-2;-1-4)=(-5;-5)
vt BC(Xc-Xb;Yc-Yb)=(-2+3;1+1)=(1;2)
vt CA(Xa-Xc;Ya-Yc)=(2+2;4-1)=(4;3)
vt AC(Xc-Xa;Yc-Ya)=(-2-2;1-4)=(-4;-3)
=>-5/-5 khác -4/-3 =>3 điểm A,B,C không thẳng hàng
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(0;2;-1),B(-2:-4;3),C(1;3;-1). Tìm điểm M ∈ O x y sao cho M A → + M B → + 3 M C → đạt giá trị nhỏ nhất.
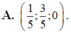
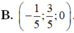
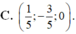
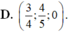
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(2;-3;7), B(0;4;-3), C(4;2;5). Tìm tọa độ điểm M trên mặt phẳng (Oxy) sao cho M A → + M B → + M C → có giá trị nhỏ nhất
A. M(-2;-1;0)
B. M(-2;-1;0)
C. M(2;-1;0)
D. M(2;1;0)
Trong mặt phẳng tọa độ với hệ tọa độ Oxy, cho hai điểm A(-2,3), B(1,-6). Tọa độ vecto AB là?
\(\overrightarrow{AB}=\left(x_B-x_A;y_B-y_A\right)=\left(3;-9\right)\)
Trong hệ tọa độ Oxy, cho hai điểm A(1; 2) ; B(- 2; 3). Tìm tọa độ đỉểm I sao cho I A → + 2 I B → = 0 → .
A. I 1 ; 2 .
B. I 1 ; 2 5 .
C. I − 1 ; 8 3 .
D. I 2 ; − 2 .
Trong hệ tọa độ Oxy cho HBH ABCD, biết A(1;3); B(-2;0), C(2;-1). Tìm tọa độ điểm D
Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A(1;2;-4); B(1;-3;1); C(2;2;3). Tính đường kính l của mặt cầu (S) đi qua ba điểm trên và có tâm nằm trên mặt phẳng (Oxy)
A. l = 2 13
B. l = 2 41
C. l = 2 26
D. l = 2 11
Đáp án C
Gọi I(x;y;0) là tâm của mặt cầu (S) ⇒ A I → = x - 1 ; y - 2 ; 4 A I → = x - 1 ; y + 3 ; - 1 A I → = x - 2 ; y - 2 ; - 3
Theo bài ra, ta có
I A = I B I A = I C ⇒ x - 1 2 + y - 2 2 + 4 2 = x - 1 2 + y + 3 2 + - 1 2 x - 1 2 + y - 2 2 + 4 2 = x - 2 2 + y - 2 2 + - 3 2 ⇔ x = - 2 y = 1
Vậy I ( - 2 ; 1 ; 0 ) ⇒ A I → = ( - 3 ; - 1 ; 4 ) ⇒ l = 2 . I A = 2 16 .
Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A(1;2;-4), B(1;-3;1), C(2;2;3). Tính đường kính l của mặt cầu (S) đi qua ba điểm trên và có tâm nằm trên mặt phẳng (Oxy).
A. I = 2 13
B. I = 2 41
C. I= 2 26
D. I= 2 11
Chọn C
Gọi tâm mặt cầu là: I(x;y;0).
I A = I B I A = I C ⇔ ( x - 1 ) 2 + ( y - 2 ) 2 + 4 2 = ( x - 1 ) 2 + ( y + 3 ) + 1 2 ( x - 1 ) 2 + ( y - 2 ) 2 + 4 2 = ( x - 2 ) 2 + ( y - 2 ) 2 + 3 2 ⇔ ( y - 2 ) 2 + 4 2 = ( y + 3 ) 2 + 1 2 x 2 - 2 x + 1 + 16 = x 2 - 4 x + 4 + 9 ⇔ 10 y = 10 2 x = - 4 ⇔ x = - 2 y = 1 ⇒ i = 2 R = 2 ( - 3 ) 2 + ( - 1 ) 2 + 4 2 = 2 26