Có bao nhiêu nghiệm phức z thỏa mãn z + i = 2 và z 2 là số thuần ảo?
A. 2
B. 4
C. 1
D. 3
PB
Những câu hỏi liên quan
Có bao nhiêu nghiệm phức z thỏa mãn |z+i| =2 và z 2 là số thuần ảo?
A. 3
B. 1
C. 4
D. 2
Có bao nhiêu số phức z thỏa mãn các điều kiện
z
-
2
+
i
2
v
à
(
z
+
i
)
2
là số thuần ảo?
Đọc tiếp
Có bao nhiêu số phức z thỏa mãn các điều kiện z - 2 + i = 2 v à ( z + i ) 2 là số thuần ảo?
Có bao nhiêu số phức z thỏa mãn: z - i = 2 và z 2 là số thuần ảo
A. 3
B. 1
C. 4
D. 2
Đáp án C
Gọi z=a+bi
Để 
là số thuần ảo
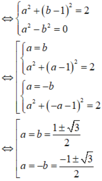
Vậy có 4 số phức thỏa mãn yêu cầu đề bài.
Đúng 0
Bình luận (0)
Có bao nhiêu số phức z thỏa mãn
z
-
i
2
v
à
z
2
là số thuần ảo
Đọc tiếp
Có bao nhiêu số phức z thỏa mãn z - i = 2 v à z 2 là số thuần ảo
Có bao nhiêu số phức z thỏa mãn: |z-i|= 2 và z 2 là số thuần ảo:
A. 3
B. 1
C. 4
D. 2
Có bao nhiêu số phức thỏa mãn
z
-
2
+
3
i
z
+
i
và
z
+
2
i
+
z
-
2
i
8
A. 0 B. 1...
Đọc tiếp
Có bao nhiêu số phức thỏa mãn z - 2 + 3 i = z + i và z + 2 i + z - 2 i = 8
A. 0
B. 1
C. 2
D. 3
Có bao nhiêu số phức \(z\) thỏa mãn \(|z|\) = \(\sqrt{2} \) và \((z+2i)(\overline{z} -2)\) là số thuần ảo ?
Đặt \(z=x+yi\Rightarrow x^2+y^2=2\)
\(\left(z+2i\right)\left(\overline{z}-2\right)=\left(x+\left(y+2\right)i\right)\left(x-2-yi\right)\)
\(=x\left(x-2\right)+y\left(y+2\right)+\left[\left(x-2\right)\left(y+2\right)-xy\right]i\)
\(=x^2+y^2-2x+2y+\left(2x-2y-4\right)i\)
Số phức đã cho thuần ảo khi \(\left\{{}\begin{matrix}x^2+y^2=2\\x^2+y^2-2x+2y=0\\2x-2y-4\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^2+y^2=2\\y=x-1\\x-y-2\ne0\end{matrix}\right.\) \(\Rightarrow\left(x;y\right)=\left(\dfrac{1+\sqrt{3}}{2};\dfrac{1-\sqrt{3}}{2}\right);\left(\dfrac{1-\sqrt{3}}{2};\dfrac{1+\sqrt{3}}{2}\right)\)
Có 2 số phức thỏa mãn
Đúng 1
Bình luận (0)
Có bao nhiêu số phức z thỏa mãn
z
-
i
2
;
z
2
là số thuần ảo?
Đọc tiếp
Có bao nhiêu số phức z thỏa mãn z - i = 2 ; z 2 là số thuần ảo?
Cho số phức z thỏa mãn ( 1 - 3i) z là số thực và 
. Hỏi có bao nhiêu số phức z thỏa mãn
A. 1
B. 2
C. 3
D. 4
Chọn B.
Gọi số phức cần tìm là z = a + bi.
Ta có ( 1 - 3i) z = ( 1 - 3i) ( a + bi)
= a + 3b - 3ai + bi = a + 3b + ( b - 3a) i
+ Do ( 1 - 3i) z là số thực nên b - 3a = 0 hay b = 3a
+ ta có 
⇔|a – 2 + (-b + 5)i| = 1
Hay ( a - 2) 2 + ( 5 - 3a) 2 = 1
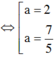(thỏa mãn)
Vậy có hai số phức z thỏa mãn là z = 2 + 6i và z = 7/5 + 21/5i
Đúng 0
Bình luận (0)