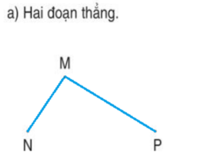
Nối các điểm để được:

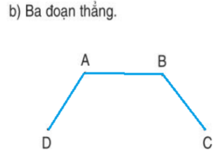
Nối các điểm để được hình có 6 cạnh
Nối các điểm để được đường gấp khúc gồm:


Phương pháp giải:
Dùng bút chì và thước kẻ, nối các điểm đã cho, sao cho tạo thành số lượng đoạn thẳng bằng với đề bài yêu cầu.
Lời giải chi tiết:
Từ hình vuông đầu tiên có cạnh bằng 1 (đơn vị độ dài), nối các trung điểm của bốn cạnh để có hình vuông thứ hai. Tiếp tục nối các trung điểm của bốn cạnh của hình vuông thứ hai để được hình vuông thứ ba. Cứ tiếp tục làm như thế, nhận được một dãy hình vuông (xem Hình 5).
a) Kí hiệu \({a_n}\) là diện tích của hình vuông thứ \(n\) và \({S_n}\) là tổng diện tích của \(n\) hình vuông đầu tiên. Viết công thức tính \({a_n},{S_n}\left( {n = 1,2,3,...} \right)\) và tìm \(\lim {S_n}\) (giới hạn này nếu có được gọi là tổng diện tích của các hình vuông).
b) Kí hiệu \({p_n}\) là chu vi của hình vuông thứ \(n\) và \({Q_n}\) là tổng chu vi của \(n\) hình vuông đầu tiên. Viết công thức tính \({p_n}\) và \({Q_n}\left( {n = 1,2,3,...} \right)\) và tìm \(\lim {Q_n}\) (giới hạn này nếu có được gọi là tổng chu vi của các hình vuông).

a) Gọi \({u_n}\) là độ dài cạnh của hình vuông thứ \(n\).
Ta có: \({u_1} = 1;{u_2} = \frac{{{u_1}}}{2}.\sqrt 2 = \frac{{{u_1}}}{{\sqrt 2 }};{u_3} = \frac{{{u_2}}}{2}.\sqrt 2 = \frac{{{u_2}}}{{\sqrt 2 }};...\)
Từ đó ta thấy \(\left( {{u_n}} \right)\) là một cấp số nhân có số hạng đầu \({u_1} = 1\), công bội \(q = \frac{1}{{\sqrt 2 }}\).
Vậy \({u_n} = {u_1}.{q^{n - 1}} = 1.{\left( {\frac{1}{{\sqrt 2 }}} \right)^{n - 1}} = \frac{1}{{{{\left( {\sqrt 2 } \right)}^{n - 1}}}},n = 1,2,3,...\)
Diện tích của hình vuông thứ \(n\) là: \({a_n} = u_n^2 = {\left( {\frac{1}{{{{\left( {\sqrt 2 } \right)}^{n - 1}}}}} \right)^2} = \frac{1}{{{2^{n - 1}}}},n = 1,2,3,...\)
Vậy \({S_n} = 1 + \frac{1}{2} + \frac{1}{{{2^2}}} + ... + \frac{1}{{{2^{n - 1}}}}\)
Đây là tổng của cấp số nhân có số hạng đầu \({u_1} = 1\), công bội \(q = \frac{1}{2}\).
Vậy \({S_n} = 1.\frac{{1 - {{\left( {\frac{1}{2}} \right)}^n}}}{{1 - \frac{1}{2}}} = 2\left( {1 - \frac{1}{{{2^n}}}} \right)\).
\(\lim {S_n} = \lim 2\left( {1 - \frac{1}{{{2^n}}}} \right) = 2\left( {1 - \lim \frac{1}{{{2^n}}}} \right) = 2\left( {1 - 0} \right) = 2\).
b) Chu vi của hình vuông thứ \(n\) là: \({p_n} = 4{u_n} = 4.\frac{1}{{{{\left( {\sqrt 2 } \right)}^{n - 1}}}} = \frac{4}{{{{\left( {\sqrt 2 } \right)}^{n - 1}}}},n = 1,2,3,...\)
Vậy \({Q_n} = 4 + \frac{4}{{\sqrt 2 }} + \frac{4}{{{{\left( {\sqrt 2 } \right)}^2}}} + ... + \frac{4}{{{{\left( {\sqrt 2 } \right)}^{n - 1}}}} = 4\left( {1 + \frac{1}{{\sqrt 2 }} + \frac{1}{{{{\left( {\sqrt 2 } \right)}^2}}} + ... + \frac{1}{{{{\left( {\sqrt 2 } \right)}^{n - 1}}}}} \right)\)
\(1 + \frac{1}{{\sqrt 2 }} + \frac{1}{{{{\left( {\sqrt 2 } \right)}^2}}} + ... + \frac{1}{{{{\left( {\sqrt 2 } \right)}^{n - 1}}}}\) là tổng của cấp số nhân có số hạng đầu \({u_1} = 1\), công bội \(q = \frac{1}{{\sqrt 2 }}\).
Vậy \(1 + \frac{1}{{\sqrt 2 }} + \frac{1}{{{{\left( {\sqrt 2 } \right)}^2}}} + ... + \frac{1}{{{{\left( {\sqrt 2 } \right)}^{n - 1}}}} = 1.\frac{{1 - {{\left( {\frac{1}{{\sqrt 2 }}} \right)}^n}}}{{1 - \frac{1}{{\sqrt 2 }}}} = \left( {2 + \sqrt 2 } \right)\left( {1 - \frac{1}{{{{\left( {\sqrt 2 } \right)}^n}}}} \right)\).
\( \Rightarrow {Q_n} = 4\left( {2 + \sqrt 2 } \right)\left( {1 - \frac{1}{{{{\left( {\sqrt 2 } \right)}^n}}}} \right)\)
\(\begin{array}{l}\lim {Q_n} = \lim 4\left( {2 + \sqrt 2 } \right)\left( {1 - \frac{1}{{{{\left( {\sqrt 2 } \right)}^n}}}} \right) = 4\left( {2 + \sqrt 2 } \right)\left( {1 - \lim \frac{1}{{{{\left( {\sqrt 2 } \right)}^n}}}} \right)\\ & = 4\left( {2 + \sqrt 2 } \right)\left( {1 - 0} \right) = 4\left( {2 + \sqrt 2 } \right)\end{array}\).
Cho tam giác đều có cạnh bằng \(a\), gọi là tam giác \({H_1}\). Nối các trung điểm của \({H_1}\) để tạo thành tam giác \({H_2}\). Tiếp theo, nối các trung điểm của \({H_1}\), để tạo thành tam giác \({H_3}\) (Hình 1). Cứ tiếp tục như vậy, nhận được dãy tam giác \({H_1},{H_2},{H_3},...\)
Tính tổng chu vi và tổng diện tích các tam giác của dãy.

Gọi \({u_n}\) là độ dài cạnh của tam giác đều thứ \(n\).
Ta có: \({u_1} = a;{u_2} = \frac{{{u_1}}}{2};{u_3} = \frac{{{u_2}}}{2};...\)
Từ đó ta thấy \(\left( {{u_n}} \right)\) là một cấp số nhân có số hạng đầu \({u_1} = a\), công bội \(q = \frac{1}{2}\).
Vậy \({u_n} = {u_1}.{q^{n - 1}} = a.{\left( {\frac{1}{2}} \right)^{n - 1}} = \frac{a}{{{2^{n - 1}}}},n = 1,2,3,...\)
Chu vi của tam giác đều thứ \(n\) là: \({p_n} = 3{u_n} = \frac{{3{\rm{a}}}}{{{2^{n - 1}}}},n = 1,2,3,...\)
Tổng chu vi của các tam giác của dãy là:
\({P_n} = 3{\rm{a}} + \frac{{3{\rm{a}}}}{2} + \frac{{3{\rm{a}}}}{{{2^2}}} + ... + \frac{{3{\rm{a}}}}{{{2^{n - 1}}}} + ... = 3{\rm{a}}\left( {1 + \frac{1}{2} + \frac{1}{{{2^2}}} + ... + \frac{1}{{{2^{n - 1}}}} + ...} \right)\)
Tổng \(1 + \frac{1}{2} + \frac{1}{{{2^2}}} + ... + \frac{1}{{{2^{n - 1}}}} + ...\) là tổng của cấp số nhân lùi vô hạn có số hạng đầu \({u_1} = 1\), công bội \(q = \frac{1}{2}\).
Vậy \(1 + \frac{1}{2} + \frac{1}{{{2^2}}} + ... + \frac{1}{{{2^{n - 1}}}} + ... = \frac{1}{{1 - \frac{1}{2}}} = 2 \Rightarrow {P_n} = 3{\rm{a}}.2 = 6{\rm{a}}\).
Diện tích của hình vuông thứ \(n\) là:
\({s_n} = \frac{{u_n^2\sqrt 3 }}{4} = {\left( {\frac{a}{{{2^{n - 1}}}}} \right)^2}.\frac{{\sqrt 3 }}{4} = \frac{{{a^2}\sqrt 3 }}{4}.{\left( {\frac{1}{{{2^{n - 1}}}}} \right)^2} = \frac{{{a^2}\sqrt 3 }}{4}.\frac{1}{{{4^{n - 1}}}},n = 1,2,3,...\)
Tổng diện tích của các tam giác của dãy là:
\({S_n} = \frac{{{a^2}\sqrt 3 }}{4} + \frac{{{a^2}\sqrt 3 }}{4}.\frac{1}{4} + \frac{{{a^2}\sqrt 3 }}{4}.\frac{1}{{{4^2}}} + ... + \frac{{{a^2}\sqrt 3 }}{4}.\frac{1}{{{4^{n - 1}}}} + ... = \frac{{{a^2}\sqrt 3 }}{4}\left( {1 + \frac{1}{4} + \frac{1}{{{4^2}}} + ... + \frac{1}{{{4^{n - 1}}}} + ...} \right)\)
Tổng \(1 + \frac{1}{4} + \frac{1}{{{4^2}}} + ... + \frac{1}{{{4^{n - 1}}}} + ...\) là tổng của cấp số nhân lùi vô hạn có số hạng đầu \({u_1} = 1\), công bội \(q = \frac{1}{4}\).
Vậy \(1 + \frac{1}{4} + \frac{1}{{{4^2}}} + ... + \frac{1}{{{4^{n - 1}}}} + ... = \frac{1}{{1 - \frac{1}{4}}} = \frac{4}{3} \Rightarrow {S_n} = \frac{{{a^2}\sqrt 3 }}{4}.\frac{4}{3} = \frac{{{a^2}\sqrt 3 }}{3}\)
cần ít nhất bao nhiêu điểm để nối lại ta được bốn hình tam giác nhận ba điểm trong các điểm trong các điểm ấy làm đình
3 điểm tạo thành 1 tam giác lớn và 1 điểm nằm giữa, nối 3 đỉnh của tam giác lớn với điểm nằm giữa ta sẽ có 4 tam giác
4 diểm 3 điểm tạo thành tam giác bự 1 điểm nằm giữa
Cho đoạn thẳng AB vẽ thêm hai điểm và nối các điểm nếu cần để được 6 đoạn thẳng
cần ít nhất bao nhiêu điểm để nối lại ta được 4 tam giác nhận 3 điểm trong các điểm ấy làm đỉnh ?
4 điểm
3 điểm tạo thành 1 tam giác lớn và 1 điểm nằm giữa, nối 3 đỉnh của tam giác lớn với điểm nằm giữa ta sẽ có 4 tam giác
Cần ít nhất bao nhiêu điểm để nối lại ta được 4 tam giác nhận 3 điểm trong các điểm ấy làm đỉnh?
cần ít nhất bao nhiêu điểm để nối lại được 4 hình tam giác nhận 3 điểm trong các điểm ấy làm đỉnh