Đạo hàm của hàm số y = s i n x 2 + 10 x là
A. cos x 2 + 10 x
B. - cos x 2 + 10 x
C. cos x 2 + 10 x 2 x 2 + 10 x
D. x + 5 cos x 2 + 10 x x 2 + 10 x
Bằng cách viết \(y = \cos x = \sin \left( {\frac{\pi }{2} - x} \right),\) tính đạo hàm của hàm số \(y = \cos x.\)
\(y'=\left(cosx\right)'\\ =\left(\dfrac{\pi}{2}-x\right)'cos\left(\dfrac{\pi}{2}-x\right)\\ =-cos\left(\dfrac{\pi}{2}-x\right)\\ =-sinx\)
Đạo hàm của hàm số y = ln 1 - c o s x là f(x). Giá trị của f(x) là :
Bình luận: Xem lại bảng công thức đạo hàm cơ bản bài 18 đề 1
A. y ' = - sin x 1 - c o s x
B. y ' = sin x 1 + c o s x
C. y ' = sin x 1 - c o s x
D. y ' = - sin x 1 + c o s x
Tính đạo hàm cấp hai của các hàm số sau:
a) \(y = {x^2} - x\);
b) \(y = \cos x\).
a: \(y'=\left(x^2-x\right)'=2x-1\)
\(y''=\left(2x-1\right)'=2\)
b: \(y'=\left(cosx\right)'=-sinx\)
\(y''=\left(-sinx\right)'=-cosx\)
Tìm đạo hàm y' của hàm số y = sin x + cos x
A. y' = 2cosx
B. y' = 2sinx
C. y' = sinx - cosx
D. y' = cosx - sinx
Cho các mệnh đề sau đây:
(1) Hàm số f ( x ) = log 2 2 x - log 2 x 4 + 4 có tập xác định D = [ 0 ; + ∞ )
(2) Hàm số y = log a x có tiệm cận ngang
(3) Hàm số y = log a x ; 0 < a < 1 và Hàm số y = log a x , a > 1 đều đơn điệu trên tập xác định của nó
(4) Bất phương trình: log 1 2 5 - 2 x 2 - 1 ≤ 0 có 1 nghiệm nguyên thỏa mãn.
(5) Đạo hàm của hàm số y = ln 1 - cos x là sin x 1 - cos x 2
Hỏi có bao nhiêu mệnh đề đúng:
A. 0
B. 2
C. 3
D.1
a) Dùng định nghĩa tỉnh đạo hàm của hàm số \(y = x\) tại điểm \(x = {x_0}\).
b) Nhắc lại đạo hàm của các hàm số \(y = {x^2},y = {x^3}\) đã tìm được ở bài học trước. Từ đó, dự đoán đạo hàm của hàm số \(y = {x^n}\) với \(n \in {\mathbb{N}^*}\).
a) Với bất kì \({x_0} \in \mathbb{R}\), ta có:
\(f'\left( {{x_0}} \right) = \mathop {\lim }\limits_{x \to {x_0}} \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} \frac{{x - {x_0}}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} 1 = 1\)
Vậy \(f'\left( x \right) = {\left( x \right)^\prime } = 1\) trên \(\mathbb{R}\).
b) Ta có:
\(\begin{array}{l}{\left( {{x^2}} \right)^\prime } = 2{\rm{x}}\\{\left( {{x^3}} \right)^\prime } = 3{{\rm{x}}^2}\\...\\{\left( {{x^n}} \right)^\prime } = n{{\rm{x}}^{n - 1}}\end{array}\)
Tính đạo hàm của hàm số sau y = sin x sin x - cos x
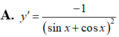
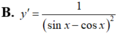
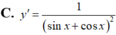

Tính đạo hàm của hàm số sau y = sin x sin x - cos x
![]()
![]()
![]()
![]()
Đạo hàm của hàm số y = cos(tan x) bằng:
A. s i n ( t a n x ) . 1 c o s 2 x
B. - s i n ( t a n x ) . 1 c o s 2 x
C. s i n ( t a n x )
D. - s i n ( t a n x )
Tính đạo hàm của hàm số y = sinx + cos x
A. sinx + cosx
B. sinx – cosx
C. cosx – sinx
D. - sinx – cosx
y ' = ( sin x + cos x ) ' y ' = ( sin x ) ' + ( cos x ) ' = c osx - sinx
Chọn đáp án C