Hãy chỉ ra kết quả sai trong việc khử giá trị tuyệt đối của tích phân sau đây:
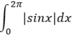
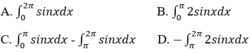
Hãy chỉ ra kết quả sai trong việc khử giá trị tuyệt đối của tích phân sau đây: ∫ 0 2 π sinx d x
A. ∫ 0 2 π sinx d x B. ∫ 0 π 2 sinx d x
C. ∫ 0 π sinx d x - ∫ π 2 π sinx d x D. - ∫ π 2 π 2 sinx d x
Phát biểu sau đây đúng hay sai ?
Muốn cộng ha số nguyên cùng dầu, ta cộng hai giá trị tuyệt đối của chúng và đặt dấu chung trước kết quả
Dùng máy tính bỏ túi hoặc bảng số để tìm giá trị của ∛12. Làm tròn kết quả nhận được đến chữ số thập phân thứ 3 và ước lượng sai số tuyệt đối.
- Dùng máy tính ta có: ∛12 ≈ 2,289428485.
- Làm tròn đến 3 chữ số phần thập phân là: ∛12 ≈ 2,289.
- Sai số tuyệt đối: Δα = |2,289 – ∛12 | < |2,289 – 2,2895| < 0,0005.
Vậy sai số tuyệt đối không vượt quá 0,0005.
cho bảng số liệu kết quả đo của 1 bịch trái cây. Hãy hoàn thành bảng số liệu và tính sai số tuyệt đối của phép đo, sai số trương đối của phép đo và viết giá trị của phép đo kèm theo sai số. Biết sai số dụng cụ là 0,1 kg
| lần đo | m(kg) | Δm(kg) |
| 1 | 3,2 | |
| 2 | 3,4 | |
| 3 | 3,4 | |
| 4 | 3,2 | |
biểu diễn kết quả đo
Một học sinh làm thí nghiệm đo bước sóng của nguồn sáng bằng thí nghiệm khe Y- âng. Giá trị trung bình và sai số tuyệt đối của phép đo khoảng cách hai khe sáng là a và ∆ a . Giá trị trung bình và sai số tuyệt đối của phép đo khoảng cách chứa hai khe đến màn đo được là D và ∆ D ; giá trị trung bình và sai số tuyệt đối của phép đo khoảng vân là i và ∆ i . Kết quả sai số tương đối của phép đo bước sóng được tính bằng:
A. ε % = ∆ a a + ∆ i i - ∆ D D . 100 %
B. ε % = ∆ a + ∆ i + ∆ D . 100 %
C. ε % = ∆ a + ∆ i - ∆ D . 100 %
D. ε % = ∆ a a + ∆ i i + ∆ D D . 100 %
Đáp án D
Biểu thức tính bước sóng là: λ = i D a
Nên ![]()
Kết quả sai số tuyệt đối của phép đo bước sóng được tính bằng: ε % = ∆ a a + ∆ i i + ∆ D D . 100 %
STUDY TIP
Tính sai số:
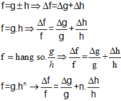
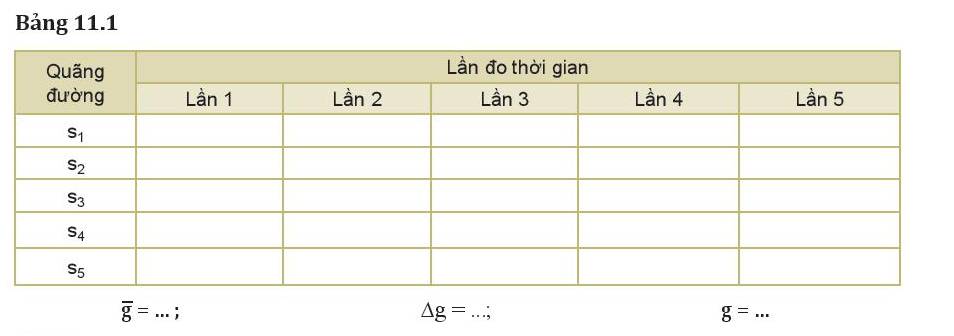
Nhận xét và đánh giá kết quả thí nghiệm:
1. Hãy tính giá trị trung bình và sai số tuyệt đối của phép đo gia tốc rơi tự do.
2. Tại sao lại dùng trụ thép làm vật rơi trong thí nghiệm? Có thể dùng viên bi thép được không? Giải thích tại sao.
3. Vẽ đồ thị mô tả mối quan hệ s và t2 trên hệ tọa độ (s – t2).
4. Nhận xét chung về dạng của đồ thị mô tả mối quan hệ s và t2 rồi rút ra kết luận về tính chất của chuyển động rơi tự do.
5. Hãy đề xuất một phương án thí nghiệm khác để đo gia tốc rơi tự do của trụ thép.
* Kết quả thí nghiệm:
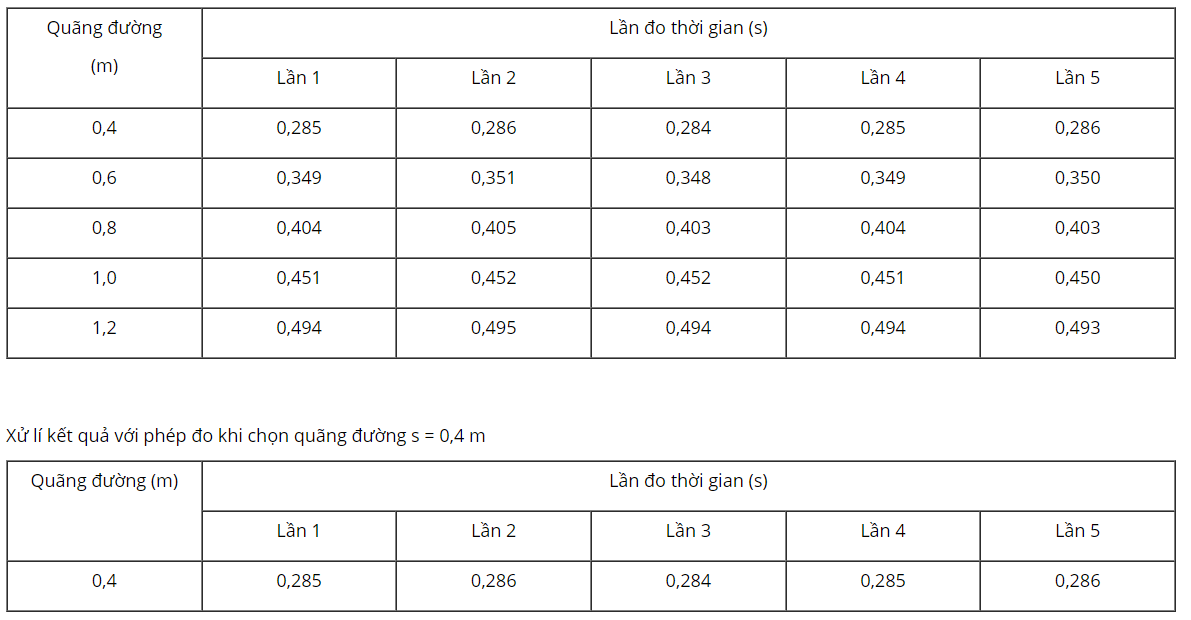
1. Tính giá trị trung bình và sai số tuyệt đối của phép đo gia tốc rơi tự do
- Lần 1: \({g_1} = \frac{{2{s_1}}}{{t_1^2}} = \frac{{2.0,4}}{{0,{{285}^2}}} = 9,849(m/{s^2})\)
- Lần 2: \({g_2} = \frac{{2{s_2}}}{{t_2^2}} = \frac{{2.0,4}}{{0,{{285}^2}}} = 9,849(m/{s^2})\)
- Lần 3: \({g_3} = \frac{{2{s_3}}}{{t_3^2}} = \frac{{2.0,4}}{{0,{{285}^2}}} = 9,919(m/{s^2})\)
- Lần 4: \({g_4} = \frac{{2{s_4}}}{{t_4^2}} = \frac{{2.0,4}}{{0,{{285}^2}}} = 9,849(m/{s^2})\)
- Lần 5: \({g_5} = \frac{{2{s_5}}}{{t_5^2}} = \frac{{2.0,4}}{{0,{{286}^2}}} = 9,780(m/{s^2})\)
Gia tốc trung bình là: \(\overline g = \frac{{9,849 + 9,849 + 9,919 + 9,849 + 9,780}}{5} = 9,849(m/{s^2})\)
Sai số tuyệt đối của gia tốc trong các lần đo
\(\begin{array}{l}\Delta {g_1} = \left| {\overline g - {g_1}} \right| = \left| {9,849 - 9,849} \right| = 0\\\Delta {g_2} = \left| {\overline g - {g_2}} \right| = \left| {9,849 - 9,849} \right| = 0\\\Delta {g_3} = \left| {\overline g - {g_3}} \right| = \left| {9,849 - 9,919} \right| = 0,07\\\Delta {g_4} = \left| {\overline g - {g_4}} \right| = \left| {9,849 - 9,849} \right| = 0\\\Delta {g_5} = \left| {\overline g - {g_5}} \right| = \left| {9,849 - 9,780} \right| = 0,069\end{array}\)
Sai số tuyệt đối trung bình là: \(\overline {\Delta g} = \frac{{\Delta {g_1} + \Delta {g_2} + \Delta {g_3} + \Delta {g_4} + \Delta {g_5}}}{5} = 0,028\)
Suy ra kết quả: \(g = 9,849 \pm 0,028\)
2. Trong thí nghiệm người ta dùng trụ thép làm vật rơi nhằm mục đích khi ta thả vật rơi thì xác suất phương rơi của vật chắn tia hồng ngoại ở cổng quang điện cao, giúp ta thực hiện thí nghiệm dễ dàng hơn
- Có thể dùng vật thả rơi là viên bi thép, nhưng xác suất khi thả rơi viên bi có phương rơi không chắn được tia hồng ngoại cao hơn khi dùng trụ thép, nên khi làm thí nghiệm với viên bi ta cần căn chỉnh và thả theo đúng phương của dây rọi.
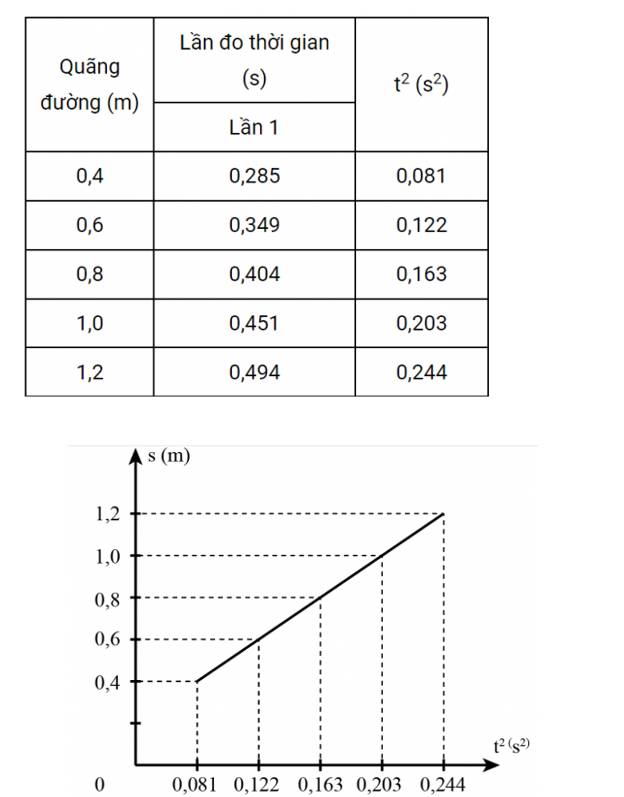
3. Xử lí số liệu và vẽ đồ thị:
Một hằng số quan trọng trong toán học là số e có giá trị gần đúng với 12 chữ số hập phân là 2,718281828459.
a) Giả sử ta lấy giá trị 2,7 làm giá trị gần đúng của e. Hãy chứng tỏ sai số tuyệt đối không vượt quá 0,02 và sai số tương đối không vượt quá 0,75%
b) Hãy quy tròn e đến hàng phần nghìn.
c) Tìm số gần đúng của số e với độ chính xác 0,00002.
a)
Sai số tuyệt đối là: \(\Delta = \left| {e - 2,7} \right| = \;|2,718281828459 - 2,7|\; = 0,018281828459 < 0,02\)
Sai số tương đối là: \({\delta _a} = \frac{{{\Delta _a}}}{{|a|}} < \frac{{0,02}}{{2,7}} \approx 0,74\% \)
b) Quy tròn e đến hàng phần nghìn ta được: 2,718.
c)
Hàng của chữ số khác 0 đầu tiên bên trái của d = 0,00002 là hàng phần trăm nghìn.
Quy tròn e đền hàng phầm trăm nghìn ta được 2,71828
Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?
a) Giá trị tuyệt đối của một số thực là một số dương.
b) Giá trị tuyệt đối của một số thực là một số không âm.
c) Giá trị tuyệt đối của một số thực là số đối của nó.
d) Hai số đối nhau có giá trị tuyệt đối bằng nhau.
a) Sai vì | 0| = 0 không phải là 1 số dương
b) Đúng
c) Sai vì giá trị tuyệt đối của một số dương là chính nó
d) Đúng
a: Sai
b: Đúng
c: Sai
d: Đúng
Dùng máy tính bỏ túi hoặc bảng số để tìm giá trị gần đúng a của \(\sqrt[3]{12}\) (kết quả được làm tròn đến chữ số thập phân thứ ba). Ước lượng sai số tuyệt đối của a ?