Cho phương trình cos5x .cosx = cos4x. cos2x + 3cos2x + 1. Các nghiệm thuộc khoảng - π ; π của phương trình là:
![]()
![]()
![]()
Tính tổng tất cả các nghiệm của phương trình cos 5 x cos x = cos 4 x cos 2 x + 3 cos 2 x + 1 thuộc khoảng - π ; π
![]()
![]()
![]()
Phương trình cos 2 x + cos x = 0 có bao nhiêu nghiệm thuộc khoảng − π ; π
A. 1
B. 4
C. 2
D. 3
Đáp án C.
Phương pháp
Sử dụng tính chất hai góc bù nhau cos x = cos π − x
Giải phương trình lượng giác cơ bản
Cách giải
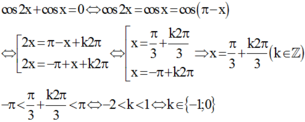
Vậy phương trình có 2 nghiệm thuộc − π ; π
Cho phương trình cos5x.cosx = cos4x.cos2x + 3cos2x + 1. Các nghiệm thuộc khoảng (-π; π) của phương trình là:
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Số nghiệm thuộc nửa khoảng [ - π ; 0 ) của phương trình cosx-cos2x-cos3x+1 = 0 là
A. 3.
B. 1.
C. 4.
D. 2.
Chọn D
Phương trình tương với:
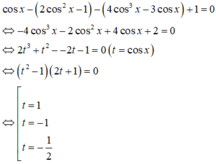
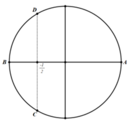
Trên đường tròn đơn vị, các điểm nghiệm của phương trình là 4 điểm A, B, C, D như hình vẽ. Do đó trên nửa khoảng [ - π ; 0 ) , phương trình có đúng 2 nghiệm (là - π và - 2 π 3 ).
Số nghiệm thuộc nửa khoảng [ − π ; 0 ) của phương trình cos x − cos 2 x − cos 3 x + 1 = 0 là
A. 3
B. 1
C. 4
D. 2
Đáp án D.
Phương trình tương với:
cos x − 2 cos 2 x − 1 − 4 cos 3 x − 3 cos x + 1 = 0 ⇔ − 4 cos 3 x − 2 cos 2 x + 4 cos x + 2 = 0 ⇔ 2 t 3 + t 2 − − 2 t − 1 = 0 t = cos x ⇔ t 2 − 1 2 t + 1 = 0 ⇔ t = 1 t = − 1 t = − 1 2
Trên đường tròn đơn vị, các điểm nghiệm của phương trình là 4 điểm A, B, C, D như hình vẽ. Do đó trên nửa khoảng − π ; 0 , phương trình có đúng 2 nghiệm (là − π và − 2 π 3 ).
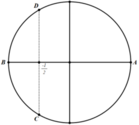
Số nghiệm của phương trình sin x sin 2 x + 2 sin x cos 2 x + sin x + cos x sin x + cos x = 3 cos 2 x trong khoảng − π ; π là:
A. 2
B. 4
C. 3
D. 5
Đáp án A
DK: sin x + cos x ≠ 0 ⇔ tan x ≠ − 1 ⇔ x ≠ − π 4 + k π
Khi đó P T ⇔ sin x sin 2 x + sin 2 x cos x + sin x + cos x sin x + cos x = 3 cos 2 x
⇔ sin x + cos x sin 2 x + 1 sin x + cos x = 3 cos 2 x − sin 2 x ⇔ sin 2 x − 2 sin x cos x + cos 2 x = 3 sin x + cos x cos x − sin x ⇔ sin x + cos x sin x + cos x = 3 sin x + cos x cos x − sin x ⇔ sin x + cos x = 3 cos x − sin x ⇔ 1 + 3 sin x = 3 − 1 cos x ⇔ tan x = 3 − 1 1 + 3 ⇔ x = π 12 + k π
có 2 nghiệm thuộc − π ; π
Số nghiệm thuộc nửa khoảng - π ; 0 của phương trình cos x - cos 2 x - cos 3 x = 0 là
![]()
![]()
![]()
![]()
Tính tổng các nghiệm thuộc khoảng 0 ; π của phương trình 4 sin 2 x 2 - 3 cos 2 x = 1 + 2 cos 2 x - 3 π 4
A. 37 π 18
B. π
C. 37 π 17
D. 3 π 2
Phương trình đã cho tương đương với
2 1 - cos x - 3 cos 2 x = 1 + 1 + cos 2 x - 3 π 2 ⇔ - 2 cos x = 3 cos 2 x - sin 2 x ⇔ - cos x = 3 2 cos 2 x - 1 2 sin 2 x ⇔ cos π - x = cos 2 x + π 6 ⇔ x = 5 π 18 + k 2 π 3 x = - 7 π 6 + k 2 π
Do x ∈ 0 ; π nên x ∈ 5 π 18 ; 17 π 18 ; 5 π 6 .
Vậy tổng các nghiệm là 37 π 18
Đáp án A
Nghiệm của phương trình cos 2 x – cos x = 0 thuộc (0;π) là:
A. x = π/2
B. x = 0
C. x = π
D. x = - π/2