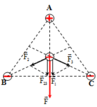
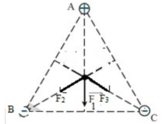
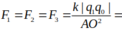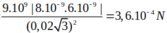Người ta đặt 3 điện tích q 1 = 8.10 − 9 C , q 2 = q 3 = − 8.10 − 9 C tại 3 đỉnh của tam giác đều ABC cạnh a = 6 cm trong không khí. Độ lớn lực tác dụng lên điện tích q 0 = 6.10 − 9 C đặt tại tâm O của tam giác là
A. 7 , 2.10 − 4 N
B. 14 , 4.10 − 4 N .
C. 4 , 8.10 − 4 N .
D. 9 , 6.10 − 4 N .