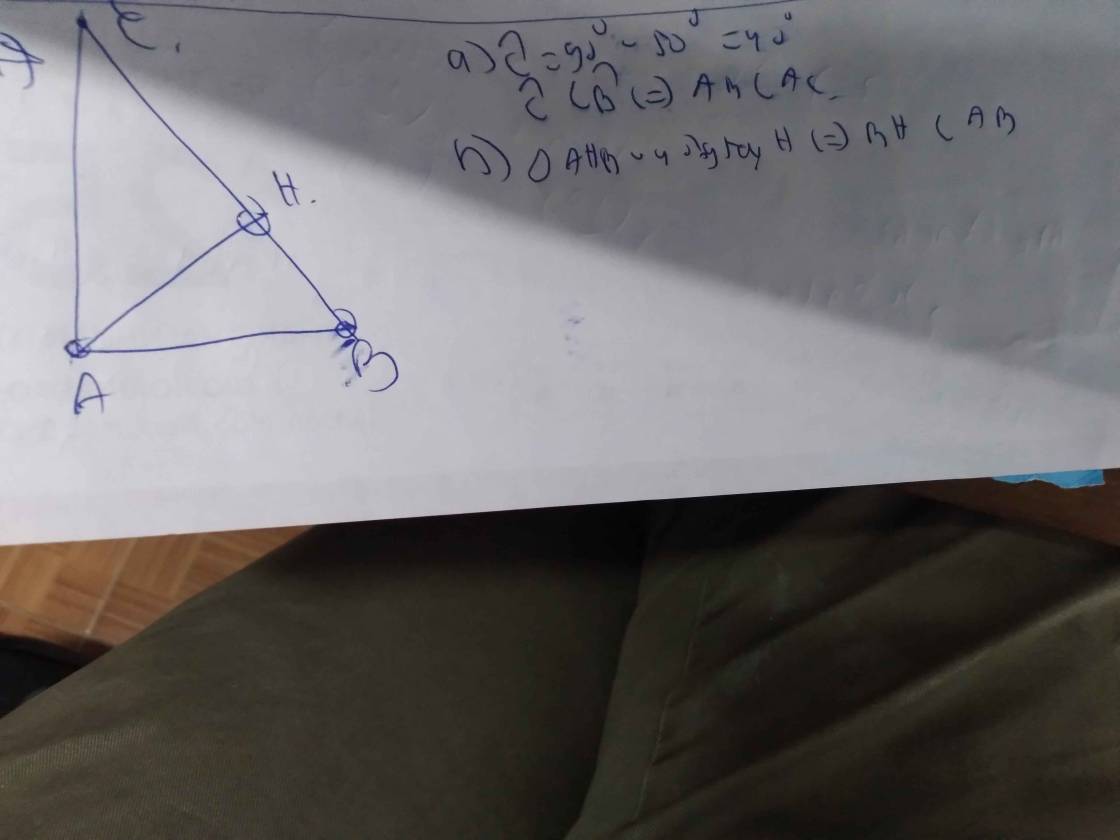
Cho tam giác ABC có ba góc nhọn, AB < AC. Kẻ AH vuông góc với BC tại H. So sánh và .
PB
Những câu hỏi liên quan
Cho tam giác ABC vuông tại A có góc B=50° a,so sánh AB và AC b,kẻ Ah vuông góc với BC tại h so sánh Bh và AB khi BC=2AB
1. cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm D. Vẽ AH vuông góc với BC tại H. So sánh HC và HD
3. cho tam giác ABC có góc B,C nhọn. Vẽ AH vuông góc với BC tại H. cm: AB+AC > 2AH
4. cho tam giác ABC nhọn. Vẽ BC vuông góc với AC tại D, vẽ CE vuông góc với AB tại E. cm: BC+CE < AB+AC
giải giúp mik với!!!! -_- "_" "_"
1. cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm D. Vẽ AH vuông góc với BC tại H. So sánh HC và HD
3. cho tam giác ABC có góc B,C nhọn. Vẽ AH vuông góc với BC tại H. cm: AB+AC > 2AH
4. cho tam giác ABC nhọn. Vẽ BC vuông góc với AC tại D, vẽ CE vuông góc với AB tại E. cm: BC+CE < AB+AC
giải giúp mik với!!!! -_- "_" "_"
1.
Ta có : AC<AD (vì : D là tia đối của tia BC )
=> HD<HC
3.
Ta có : AB+AC>AH (vì : tog 2 cah cua tam giác luôn lớn hơn cah con lại)
Mà : 1/2AH<AB+AC
=> AB+AC>2AH
4.
Ta có : ko hiu
Đúng 0
Bình luận (0)
bạn giải bài 3 mik hk hiu, bn viết rõ rak dc hk
Đúng 0
Bình luận (0)
cho tam giác ABC cân tại A, kẻ AH vuông góc với BC (H thuộc BC), kẻ AD vuông góc với AB (H thuộc AB), kẻ AE vuông góc với AC (E thuộc AC). Hãy so sánh HD và HC
Xét ΔDBH vuông tại D và ΔECH vuông tại E có
BH=CH
\(\widehat{B}=\widehat{C}\)
Do đó: ΔDBH=ΔECH
Suy ra: HD=HE
mà HE<HC
nên HD<HC
Đúng 1
Bình luận (0)
Xét ΔDBH và ΔECH có
\(\widehat{BDH}=\widehat{CEH=90^0}\)
BH=CH
\(\widehat{C}=\widehat{B}\)
=>ΔDBH=ΔECH(c.h-c.n)
=> HD=HE
mà HE<HC
nên HD<HC
Đúng 0
Bình luận (0)
Bài 5: Cho tam giác ABC có ba góc nhọn, AB<AC. Kẻ BD vuông góc với AC tại D, CE vuông góc với AB tại E. Gọi H là giao điểm của BD và CE. So sánh độ dài HB và HC.
Bài 6: Cho tam giác ABC có AB<AC. Tia phân giác của góc B và C cắt nhau tại I. Từ I vẽ IH vuông góc với BC. So sánh độ dài HB và HC.
Câu hỏi là j vậy bn ?
what the hell??????
Bài 5: Cho tam giác ABC có ba góc nhọn, AB<AC. Kẻ BD vuông góc với AC tại D, CE vuông góc với AB tại E. Gọi H là giao điểm của BD và CE. So sánh độ dài HB và HC.
Bài 6: Cho tam giác ABC có AB<AC. Tia phân giác của góc B và C cắt nhau tại I. Từ I vẽ IH vuông góc với BC. So sánh độ dài HB và HC.
~~~Đây,các bạn giúp mk vs~~~
Bài 5: Cho tam giác ABC có ba góc nhọn, AB<AC. Kẻ BD vuông góc với AC tại D, CE vuông góc với AB tại E. Gọi H là giao điểm của BD và CE. So sánh độ dài HB và HC.
Bài 6: Cho tam giác ABC có AB<AC. Tia phân giác của góc B và C cắt nhau tại I. Từ I vẽ IH vuông góc với BC. So sánh độ dài HB và HC.
Bài 5: Cho tam giác ABC có ba góc nhọn, AB<AC. Kẻ BD vuông góc với AC tại D, CE vuông góc với AB tại E. Gọi H là giao điểm của BD và CE. So sánh độ dài HB và HC.
Bài 6: Cho tam giác ABC có AB<AC. Tia phân giác của góc B và C cắt nhau tại I. Từ I vẽ IH vuông góc với BC. So sánh độ dài HB và HC.
Bạn viết đề bài cho đầy đủ chứ -.-
~ Vào thông kê của bạn ý là thấy đề ~
Bài 5:
Bài làm
Xét tam giác ABC có:
AB < AC (gt)
=> \(\widehat{ABC}>\widehat{ACB}\)( Quan hệ giữa góc và cạnh đối diện ) (1)
Xét tam giác EBC vuông ở E có:
\(\widehat{ABC}+\widehat{ECB}=90^0\) (2)
Xét tam giác DBC vuông ở D có:
\(\widehat{ACB}+\widehat{DBC}=90^0\) (3)
Từ (1) , (2) và (3) => \(\widehat{ECB}< \widehat{DBC}\)
Xét tam giác HBC có:
\(\widehat{ECB}< \widehat{DBC}\) ( theo quan hệ giữa góc và cạnh đối diện có )
BH < HC
Vậy BH < HC
Bài 6
Bài làm:
Xét tam giác ABC có:
AB < AC ( gt )
\(\widehat{ABC}>\widehat{ACB}\)( quan hệ giữa góc và cạnh đối diện ) (1)
Mà BI là phân giác góc ABC
=> \(\frac{1}{2}\widehat{ABC}=\widehat{ABI}=\widehat{IBC}\) (2)
Và CI là phân giác góc ACB
=> \(\frac{1}{2}\widehat{ACB}=\widehat{ACI}=\widehat{ICB}\) (3)
Từ (1), (2) và (3) => \(\widehat{ABI}=\widehat{IBC}>\widehat{ACI}=\widehat{ICB}\) (4)
Xét tam giác IHB vuông ở H có:
\(\widehat{IBC}+\widehat{BIH}=90^0\) (5)
Xét tam giác IHC vuông ở H có:
\(\widehat{ICB}+\widehat{CIH}=90^0\) (6)
Từ (4), (5) và (6) => \(\widehat{BIH}< \widehat{CIH}\)
Xét tam giác IBC có:
\(\widehat{BIH}< \widehat{CIH}\)( Theo quan hệ giữa góc đối và cạnh đối diện có: )
BH < HC
Vậy BH < HC
# Học tốt #
Cho tam giác ABC vuông tại A, kẻ AH vuông góc với BC (H thuộc BC). Trên BC lấy điểm D sao cho BD=BA.
a. CMR: Tia AD là phân giác góc HAC
b. Kẻ DK vuông góc AC (K thuộc AC). CMR: Tam giác AHD = tam giác AKD
c. So sánh AC - AH với BC - AB
Cho tam giác ABC vuông tại A, kẻ AH vuông góc với BC (H thuộc BC). Trên BC lấy điểm D sao cho BD=BA.
a. CMR: Tia AD là phân giác góc HAC
b. Kẻ DK vuông góc AC (K thuộc AC). CMR: Tam giác AHD = tam giác AKD
c. So sánh AC - AH với BC - AB
Cho tam giác nhọn có AB<AC;AH vuông góc với BC( H thuộc BC ). a) So sánh HB với CH; AB với AH. So sánh BH với AB+AC với BC. Kẻ BC vuông góc với AC ( K thuộc AC). Gọi I là giao điểm của AH và BK. Chứng minh CI vuông góc với AB
Cho tam giác nhọn có AB<AC;AH vuông góc với BC( H thuộc BC )
a) So sánh HB với CH; AB với AH. So sánh BH với AB+AC với BC.
b) Kẻ BC vuông góc với AC ( K thuộc AC). Gọi I là giao điểm của AH và BK. Chứng minh CI vuông góc với AB
Đúng 0
Bình luận (0)