Tìm phương trình chính tắc của Elip có một đường chuẩn là x+ 4 0 và một tiêu điểm là điểm (-1; 0) .
Đọc tiếp
Tìm phương trình chính tắc của Elip có một đường chuẩn là x+ 4= 0 và một tiêu điểm là điểm (-1; 0) .
PB
Những câu hỏi liên quan
Cho elip (E) có một đỉnh là A( 5; 0) và có 1 tiêu điểm F1(- 4; 0). Phương trình chính tắc của elip là: A.
x
2
25
+
y
2
16
1.
B.
x
2
5
+
y
2
4
1.
C. ...
Đọc tiếp
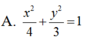
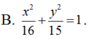
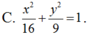
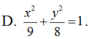
Cho elip (E) có một đỉnh là A( 5; 0) và có 1 tiêu điểm F1(- 4; 0). Phương trình chính tắc của elip là:
A. x 2 25 + y 2 16 = 1.
B. x 2 5 + y 2 4 = 1.
C. x 2 25 + y 2 9 = 1.
D. x 5 + y 4 = 1.
Phương trình chính tắc của elip có một tiêu điểm
F
1
2
;
0
và đi qua điểm
M
2
;
1
là
Đọc tiếp
Phương trình chính tắc của elip có một tiêu điểm F 1 2 ; 0 và đi qua điểm M 2 ; 1 là
Lập phương trình chính tắc của elip trong trường hợp sau: Elip có một tiêu điểm là
F
1
-
3
;
0
và điểm
M
1
;
3
2
nằm trên elip...
Đọc tiếp
Lập phương trình chính tắc của elip trong trường hợp sau: Elip có một tiêu điểm là F 1 - 3 ; 0 và điểm M 1 ; 3 2 nằm trên elip.
Gọi Elip cần tìm có dạng : (E) :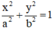 
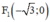là tiêu điểm của (E) ⇒ a2 – b2 = 3 ⇒ a2 = b2 + 3
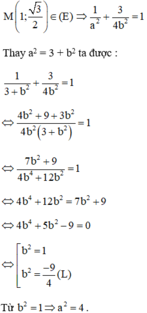
Phương trình chính tắc của Elip là :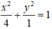 
Đúng 1
Bình luận (0)
Elip có một tiêu điểm F(-2; 0) và tích độ dài trục lớn với trục bé bằng
12
5
. Phương trình chính tắc của elip là: A.
x
2
9
+
y
2
5
1.
B.
x
2
36
+
y
2
20...
Đọc tiếp
Elip có một tiêu điểm F(-2; 0) và tích độ dài trục lớn với trục bé bằng 12 5 . Phương trình chính tắc của elip là:
A. x 2 9 + y 2 5 = 1.
B. x 2 36 + y 2 20 = 1.
C. x 2 144 + y 2 5 = 1.
D. x 2 45 + y 2 16 = 1.
Cho elip (E) có các tiêu điểm
F
1
-
5
;
0
,
F
2
5
;
0
và một điểm M nằm trên (E) sao cho chu vi của tam giác
M
F
1
F
2
bằng 30. Khi đó phương trình chính tắc của elip là: A. ...
Đọc tiếp
Cho elip (E) có các tiêu điểm F 1 - 5 ; 0 , F 2 5 ; 0 và một điểm M nằm trên (E) sao cho chu vi của tam giác M F 1 F 2 bằng 30. Khi đó phương trình chính tắc của elip là:
A. x 2 75 + y 2 100 = 1
B. 100 x 2 + 75 y 2 = 1
C. 75 x 2 + 100 y 2 = 1
D. x 2 100 + y 2 75 = 1
Viết phương trình chính tắc của elip đi qua điểm A(0;-4) và có 1 tiêu điểm F2(3;0)
Gọi ptr chính tắc của `(E)` có dạng: `[x^2]/[a^2]+[y^2]/[b^2]=1`
Thay `A(0;-4)` vào `(E)` có:
`16/[b^2]=1<=>b^2=16`
Vì `F_2 (3;0)=>c=3=>c^2=9`
Ta có: `a^2=b^2+c^2`
`<=>a^2=16+9`
`<=>a^2=25`
Vậy ptr chính tắc của `(E)` là: `[x^2]/25+[y^2]/16=1`
Đúng 2
Bình luận (0)
Viết phương trình chính tắc của elip đi qua điểm A(0;-4) và có 1 tiêu điểm F2(3;0)
viết phương trình chính tắc của elip đi qua điểm A(0;-4) và có 1 tiêu điểm F2(3;0)
\(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\)(E)
Thay x=0 và y=-4 vào (E), ta được:
16/b^2=1
=>b=4
F2(3;0)
=>c=3
=>căn a^2-16=3
=>a^2-16=9
=>a=5
=>x^2/25+y^2/16=1
Đúng 1
Bình luận (0)
Cho elip có phương trình chính tắc \(\frac{{{x^2}}}{{100}} + \frac{{{y^2}}}{{64}} = 1\). Tìm các tiêu điểm và tiêu cự của elip.
Ta có: \(c = \sqrt {{{100}^2} - {{64}^2}} = 6\). Do đó (E) có hai tiêu điểm là \({F_1}\left( { - 6;0} \right),{F_2}\left( {6;0} \right)\) và có tiêu cự bằng 2c = 12.
Đúng 0
Bình luận (0)